
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,数列
,数列![]() 的通项公式为
的通项公式为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
①求![]() ;
;
②若![]() ,求数列
,求数列![]() 的最小项的值.
的最小项的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)由![]() 与
与![]() 的关系得
的关系得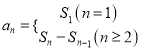 ,又
,又![]() ,
,
![]() ;(2)由(1)得
;(2)由(1)得![]() ,讨论
,讨论![]() 分别用公式法和错误相减法求和;
分别用公式法和错误相减法求和;
![]() 时,
时, ![]() =
=![]() ,构造函数研究单调性得最小值
,构造函数研究单调性得最小值
(1)an=![]() =2n.…………………4分
=2n.…………………4分
(若没有交待a1扣1分)
(2)cn=![]() .
.
Tn=2+4x+6x2+8x3+……+![]() . ①
. ①
则xTn=2x+4x2+6x3+8x3+……+![]() . ②
. ②
①-②,得(1-x)Tn=2+2x+2x2+……+![]() -
-![]() .
.
当x≠1时,(1-x)Tn=2×![]() -
-![]() .所以Tn=
.所以Tn=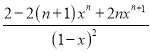 .…8分
.…8分
当x=1时,Tn=2+4+6+8+……+2n=n2+n.…………………10分
(3)当x=2时,Tn=2+![]() .
.
则![]() =
=![]() . ……………………11分
. ……………………11分
设f(n)=![]() .
.
因为f(n+1)-f(n)=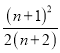 -
-![]() =
=![]() >0, …………14分
>0, …………14分
所以函数f(n)在n∈N+上是单调增函数. …………………15分
所以n=1时,f(n)取最小值![]() ,即数列{
,即数列{![]() }的最小项的值为
}的最小项的值为![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn=﹣3n2+49n.
(1)请问数列{an}是否为等差数列?如果是,请证明;
(2)设bn=|an|,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)在定义域上存在区间[a,b](ab>0),使f(x)在[a,b]上值域为[ ![]() ],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+
],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+ ![]() ②f(x)=﹣x2+4x ③f(x)=sin
②f(x)=﹣x2+4x ③f(x)=sin ![]() x ④f(x)=
x ④f(x)= 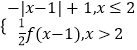 ,具有“反衬性”的为|( )
,具有“反衬性”的为|( )
A.②③
B.①③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于两点A,B,当![]() 时,求直线斜率的取值范围.
时,求直线斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
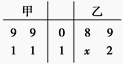
【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线![]() 相切.
相切.
(1)求直线![]() 被圆
被圆![]() 所截得的弦
所截得的弦![]() 的长;
的长;
(2)过点![]() 作两条与圆
作两条与圆![]() 相切的直线,切点分别为
相切的直线,切点分别为![]() 求直线
求直线![]() 的方程;
的方程;
(3)若与直线![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 为钝角,求直线
为钝角,求直线![]() 在
在![]() 轴上的截距的取值范围.
轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a、b、c成等比数列,非零实数x,y分别是a与b,b与c的等差中项.
(1)已知 ①a=1、b=2、c=4,试计算 ![]() 的值;
的值;
②a=﹣1、b= ![]() 、c=﹣
、c=﹣ ![]() ,试计算
,试计算 ![]() 的值
的值
(2)试推测 ![]() 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com