
【题目】设a、b、c成等比数列,非零实数x,y分别是a与b,b与c的等差中项.
(1)已知 ①a=1、b=2、c=4,试计算 ![]() 的值;
的值;
②a=﹣1、b= ![]() 、c=﹣
、c=﹣ ![]() ,试计算
,试计算 ![]() 的值
的值
(2)试推测 ![]() 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
【答案】
(1)解:①a、b、c成等比数列,
非零实数x,y分别是a与b,b与c的等差中项.
可得b2=ac,x= ![]() ,y=
,y= ![]() ,
,
由a=1、b=2、c=4,
可得x= ![]() ,y=3,
,y=3,
即有 ![]() =
= ![]() +
+ ![]() =2;
=2;
②由a=﹣1、b= ![]() 、c=﹣
、c=﹣ ![]() ,
,
可得x=- ![]() ,y=
,y= ![]() ,
,
∴ ![]() =3﹣1=2
=3﹣1=2
(2)解:由(1)推测 ![]() =2.
=2.
证明:∵a、b、c成等比数列,∴b2=ac,
∵实数x,y分别是a与b,b与c的等差中项.
∴x= ![]() ,y=
,y= ![]()
∴ ![]() =
= ![]()
= ![]()
= ![]()
【解析】(1)由等差数列和等比数列的中项的性质,可得b2=ac,x= ![]() ,y=
,y= ![]() ,代入a,b,c可得x,y,计算即可得到①②的值;(2)推测
,代入a,b,c可得x,y,计算即可得到①②的值;(2)推测 ![]() =2.运用等差数列和等比数列的中项的性质,通分化简,运用因式分解,注意运用ac=b2 , 即可得证.
=2.运用等差数列和等比数列的中项的性质,通分化简,运用因式分解,注意运用ac=b2 , 即可得证.
【考点精析】通过灵活运用基本不等式和等差数列的通项公式(及其变式),掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ;通项公式:
;通项公式:![]() 或
或![]() 即可以解答此题.
即可以解答此题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,且a3=﹣6,a6=0.
(1)求{an}的通项公式.
(2)若等比数列{bn}满足b1=8,b2=a1+a2+a3 , 求{bn}的前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为
为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医生的专业能力参数![]() 可有效衡量医生的综合能力,
可有效衡量医生的综合能力,![]() 越大,综合能力越强,并规定: 能力参数
越大,综合能力越强,并规定: 能力参数![]() 不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力
不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力![]() 的频率分布直方图:
的频率分布直方图:
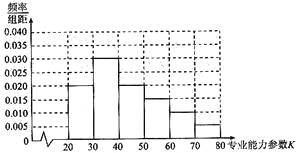
(Ⅰ)求出这个样本的合格率、优秀率;
(Ⅱ)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名.
①求这2名医生的能力参数![]() 为同一组的概率;
为同一组的概率;
②设这2名医生中能力参数![]() 为优秀的人数为
为优秀的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,应沿什么方向,用多少h能尽快追上乙船?
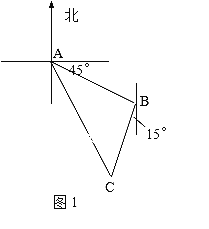
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com