
����Ŀ��ҽ����רҵ��������![]() ����Ч����ҽ�����ۺ�������
����Ч����ҽ�����ۺ�������![]() Խ���ۺ�����Խǿ�����涨: ��������
Խ���ۺ�����Խǿ�����涨: ��������![]() ������30��Ϊ�ϸ�����50��Ϊ���㣮ij�������������������ȡ300��ҽ������רҵ�����������ˣ��õ���ͼ��ʾ������
������30��Ϊ�ϸ�����50��Ϊ���㣮ij�������������������ȡ300��ҽ������רҵ�����������ˣ��õ���ͼ��ʾ������![]() ��Ƶ�ʷֲ�ֱ��ͼ:
��Ƶ�ʷֲ�ֱ��ͼ:
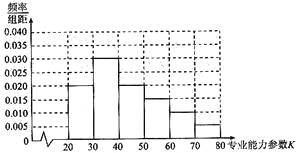
�����������������ĺϸ��ʡ������ʣ�
���������÷ֲ�����ķ������г��һ����������Ϊ20���������ٴ���20��ҽ�������ѡ��2����
������2��ҽ������������![]() Ϊͬһ��ĸ��ʣ�
Ϊͬһ��ĸ��ʣ�
������2��ҽ������������![]() Ϊ���������Ϊ
Ϊ���������Ϊ![]() �����������
�����������![]() �ķֲ��к�������
�ķֲ��к�������
���𰸡���1�������Ƶ������Ϊ0.2��0.3��0.2��0.15��0.1��0.05��
![]() ��������ĺϸ���Ϊ1��0.2=0.8��������Ϊ0.15+0.1+0.05=0.3��
��������ĺϸ���Ϊ1��0.2=0.8��������Ϊ0.15+0.1+0.05=0.3��
��������K��ƽ��ֵΪ25��0.2+35��0.3+45��0.2+55��0.15+65��0.1+75��0.05="43."
��2���ֲ���Ϊ
X | 0 | 1 | 2 |
P |
|
|
|
![]() ������ֵ
������ֵ![]() .
.
�������������������1����Ƶ�ʷֲ�ֱ��ͼ���ϸ����ǣ� ![]()
�������ǣ� ![]()
��2����Ƶ�ʷֲ�ֱ��ͼ�������20��ҽ���У����������ֱ�Ϊ4�ˣ�6�ˣ�4�ˣ�3�ˣ�2�ˣ�1��
���ɹŵ�������
�����������Ϊ��3+2+1��6�ˣ� ![]() �÷ֲ��У����������� ��
�÷ֲ��У����������� ��
�����������1���ϸ����ǣ� ![]()
�������ǣ� ![]()
��2��������֪����20��ҽ���У�[20��30]��4�ˣ�[30��40]��6�ˣ�[40��50]��4�ˣ�[50��60]��3�ˣ�[60��70]��2�ˣ�[70��80]��1��
��![]()
�������������3+2+1��6��
![]()
![]() ��
�� ![]()
![]() �ķֲ����ǣ�
�ķֲ����ǣ�
| 0 | 1 | 2 |
|
|
|
|
��![]() ��������
��������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����β���ʽax2+bx+1��0�Ľ⼯Ϊ{x|��1��x�� ![]() }����ab��ֵΪ�� ��
}����ab��ֵΪ�� ��
A.��5
B.5
C.��6
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������㷨ͳ�ڡ������������⣺��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ�ƣ�����˼�ǣ�һ��7����������381յ�ƣ������������е���һ���������һ�������2���������Ķ��㹲�еƣ� ��
A. 1յ B. 3յ C. 5յ D. 9յ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��c�ɵȱ����У�����ʵ��x��y�ֱ���a��b��b��c�ĵȲ����
��1����֪ ��a=1��b=2��c=4���Լ��� ![]() ��ֵ��
��ֵ��
��a=��1��b= ![]() ��c=��
��c=�� ![]() ���Լ���
���Լ��� ![]() ��ֵ
��ֵ
��2�����Ʋ� ![]() ��2�Ĵ�С��ϵ����֤����Ľ��ۣ�
��2�Ĵ�С��ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�����ڶ�ͬһ���![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���������Ʒ��ֻ��һ��һ�Ƚ�������������ǰ���ס��ҡ���������λͬѧ�������������Ʒ�����Ԥ�����£�
���������Ʒ��ֻ��һ��һ�Ƚ�������������ǰ���ס��ҡ���������λͬѧ�������������Ʒ�����Ԥ�����£�
��˵����![]() ��
��![]() ��Ʒ���һ�Ƚ���
��Ʒ���һ�Ƚ���
��˵����![]() ��Ʒ���һ�Ƚ���
��Ʒ���һ�Ƚ���
��˵����![]() ��
�� ![]() ������Ʒδ���һ�Ƚ���
������Ʒδ���һ�Ƚ���
��˵����![]() ��Ʒ���һ�Ƚ�����
��Ʒ���һ�Ƚ�����
������λͬѧ��ֻ����λ˵�Ļ��ǶԵģ�����һ�Ƚ�����Ʒ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(3,5)��B(��1,3)��C(��3,1)Ϊ��ABC���������㣬O��M��N�ֱ�Ϊ��AB��BC��CA���е㣬���OMN�����Բ�ķ��̣��������Բ��Բ�ĺͰ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin����x+�գ���A��0��|��|�� ![]() �����е�ͼ����ͼ��ʾ��Ϊ�˵õ�g��x��=cos��2x��
�����е�ͼ����ͼ��ʾ��Ϊ�˵õ�g��x��=cos��2x�� ![]() ����ͼ��ֻ�轫f��x����ͼ�� ��
����ͼ��ֻ�轫f��x����ͼ�� �� 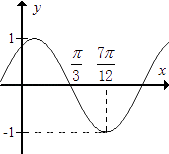
A.����ƽ�� ![]() ����λ
����λ
B.����ƽ�� ![]() ����λ
����λ
C.����ƽ�� ![]() ����λ
����λ
D.����ƽ�� ![]() ����λ
����λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
�� ![]() .
.
��1���躯��![]() ����
����![]() ������
������![]() �ϵ�������ʵ��
�ϵ�������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����⽨��һ����������ݣ���ȡ����ķ�ʽ�Ӷ�ҽ�����˾ѡȡһ�ҽ�����˾���������ɸѡ���ס������ҽ�����˾���������б�.�ִӽ������ԺƸ��ר�������һ���б귽��:���ҹ�˾��![]() ���б������������ȡ
���б������������ȡ![]() �����⣬��֪��
�����⣬��֪��![]() ���б������У���˾����ȷ�ش����е�
���б������У���˾����ȷ�ش����е�![]() ���}Ŀ�����ҹ�˾����ȷ�ش���Ŀ�ĸ��ʾ�Ϊ
���}Ŀ�����ҹ�˾����ȷ�ش���Ŀ�ĸ��ʾ�Ϊ![]() ���ס������ҹ�˾��ÿ��Ļش��������������Ӱ���.
���ס������ҹ�˾��ÿ��Ļش��������������Ӱ���.
��1����ס������ҹ�˾�����![]() ����Ŀ�ĸ��ʣ�
����Ŀ�ĸ��ʣ�
��2����������ͷ���ĽǶȷ������ס��������ļҹ�˾����ɹ��Ŀ����Ը���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com