
【题目】函数f(x)=Asin(ωx+φ)(A>0,|φ|< ![]() )其中的图象如图所示,为了得到g(x)=cos(2x﹣
)其中的图象如图所示,为了得到g(x)=cos(2x﹣ ![]() )的图象,只需将f(x)的图象( )
)的图象,只需将f(x)的图象( ) 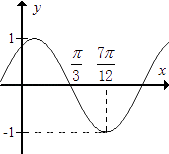
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
【答案】D
【解析】解:∵由函数图象可得:A的值为1,周期T=4×( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴ω= ![]() =
= ![]() =2,
=2,
又函数的图象的第二个点是( ![]() ,0),
,0),
∴2× ![]() +φ=π,
+φ=π,
于是φ= ![]() ,则f(x)=sin(2x+
,则f(x)=sin(2x+ ![]() )=sin[2(x+
)=sin[2(x+ ![]() )],
)],
∵g(x)=cos(2x﹣ ![]() )=sin2x,
)=sin2x,
∴为了得到g(x)=cos(2x﹣ ![]() )的图象,只需将f(x)的图象向右平移
)的图象,只需将f(x)的图象向右平移 ![]() 个单位即可.
个单位即可.
故选:D.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】为了提高产品的年产量,某企业拟在2013年进行技术改革,经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3﹣ ![]() (k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(1)试确定k的值,并将2013年该产品的利润y万元表示为技术改革费用m万元的函数(利润=销售金额﹣生产成本﹣技术改革费用);
(2)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医生的专业能力参数![]() 可有效衡量医生的综合能力,
可有效衡量医生的综合能力,![]() 越大,综合能力越强,并规定: 能力参数
越大,综合能力越强,并规定: 能力参数![]() 不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力
不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力![]() 的频率分布直方图:
的频率分布直方图:
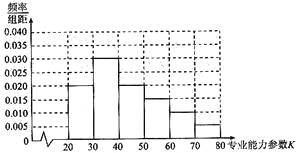
(Ⅰ)求出这个样本的合格率、优秀率;
(Ⅱ)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名.
①求这2名医生的能力参数![]() 为同一组的概率;
为同一组的概率;
②设这2名医生中能力参数![]() 为优秀的人数为
为优秀的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的圆形纸板内有一个相同圆心的半径为
的圆形纸板内有一个相同圆心的半径为![]() 的小圆,现将半径为
的小圆,现将半径为![]() 的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 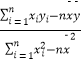 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
参考数据:7×165+6×142+6×148+5×125+6×150=4420.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的空间几何体中,底面四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
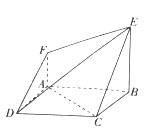
(1)求二面角![]() 的大小;
的大小;
(2)若在平面![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,试通过计算说明点
,试通过计算说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择.
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(1)求某员工选择方案甲进行抽奖所奖金![]() (元)的分布列;
(元)的分布列;
(2)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com