
【题目】已知二次函数![]() 的两个零点为
的两个零点为![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试判断点
,试判断点![]() 是否在直线
是否在直线![]() 上? 并说明理由.
上? 并说明理由.
【答案】(I)![]() ;(II)点
;(II)点![]() 在直线
在直线![]() 上.
上.
【解析】
(Ⅰ)运用二次方程的判别式大于0,结合二次不等式的解法,即可得到所求范围;
(Ⅱ)若a>c,则b>0,化简可得g(x)=2ax2+4bx+![]() ,讨论a的符号和最大值的取得,解方程即可得到结论.
,讨论a的符号和最大值的取得,解方程即可得到结论.
解:(Ⅰ)因为二次函数![]() 的两个零点为
的两个零点为![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
又![]() ,即
,即![]() ,
,
所以![]() .
.
故![]() ,即
,即![]() ,
,
得![]() .
.
解得![]() 或
或![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)依题意,![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
则![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
由于![]() ,则
,则![]() .
.
①若![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,得
,得![]() ,
,
则二次函数![]() 区间
区间![]() 上单调递增.
上单调递增.
故函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
依题意,得![]() ,化为
,化为![]() ,
,
由于![]() ,则
,则![]() .
.
②若![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,得
,得![]() ,
,
则二次函数![]() 区间
区间![]() 上单调递增.
上单调递增.
故函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
依题意,得![]() ,化为
,化为![]() ,
,
由![]() ,得
,得![]() ,则
,则![]() .
.
故![]() .
.
综合①②知![]() ,
,
所以点![]() 在直线
在直线![]() 上
上


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,1].
(1)求m的值;
(2)若a,b,c∈R,且 ![]() =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线, ![]() ,
,![]() 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
A. 若![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]()
B. 若![]() ,
,![]() ,
,![]() ,则
,则![]()
C. 若![]() ∥
∥![]() ,
,![]() ,
,![]()
![]()
![]() ,则
,则![]()
D. 若![]() ∥
∥![]() ,
,![]()
![]()
![]() ,
,![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
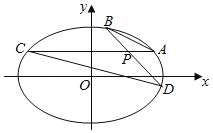
【题目】已知椭圆![]() ,倾斜角为
,倾斜角为![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .过椭圆
.过椭圆![]() 内一点
内一点![]() 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点![]() ,且满足
,且满足![]() ,其中
,其中![]() 为实数.当直线
为实数.当直线![]() 平行于
平行于![]() 轴时,对应的
轴时,对应的![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,
变化时,![]() 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2﹣a),a∈R.
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若函数f(x)在(﹣3,0)上单调递减,试求a的取值范围;
(3)若函数f(x)的最小值为﹣2e,试求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() (a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
(a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
A.(3,+∞)
B.(0, ![]() ]
]
C.(1,3)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48. 
(1)求an1和a4n;
(2)设bn= ![]() +(﹣1)na
+(﹣1)na ![]() (n∈N+),求数列{bn}的前n项和Sn .
(n∈N+),求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com