
在平面直角坐标系中,O是坐标原点,两定点A,B满足| |=|
|=| |=
|= ·
· =2,则点集{P|
=2,则点集{P| =λ
=λ +μ
+μ ,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( ).
,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( ).
A.2 B.2
B.2 C.4
C.4 D.4
D.4
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评3练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C对应的边分别是 a,b,c.已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评1练习卷(解析版) 题型:填空题
给定区域D: .令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定________条不同的直线.
.令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定________条不同的直线.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练9练习卷(解析版) 题型:填空题
设数列{an}是公差不为0的等差数列,a1=1且a1,a3,a6成等比数列,则数列{an}的前n项和Sn=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练8练习卷(解析版) 题型:解答题
A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
(1)求 ·
· +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:解答题
△ABC中内角A,B,C的对边分别为a,b,c,已知a=bcos C+csin B.
(1)求B;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:选择题
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知8b=5c,C=2B,则cos C等于( ).
A. B.-
B.- C.±
C.± D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知倾斜角为α的直线l与直线x-2y+2=0平行,则tan 2α的值为( ).
A.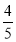 B.
B. C.
C.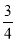 D.
D.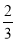
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com