练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a∈R,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数。


    f’(x)=ex(a2+ax+a+1)+ex(2x+a)=ex[x2+(a+2)x+(2a+1)]

    令f’(x)=0得x2+(a+2)x+(2a+1)=0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    将标号为1、2，… 10的10个数放入标号为1，2，…10的10个盒子内，每一个盒内放一个球茎，恰在此时好有3个球的标号与其所在盒子的标号不一致的放入方法种数为  （  ）

      A．120     B．240     C．360      D．720

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数z=1+i，求实数a、b,使az+2b=(a+2z)2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果复数是实数，则实数

    A．               B．           C．             D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f0(x)=sinx,f1(x)=f’0(x),f2(x)=f’1(x),…,fn+1(x)=f’n(x),n∈N,则f2005(x)    (   )

    A.sinx            B.-sinx         C.cosx       D.-cosx

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)在x=1处的导数为1，则等于    （  ）]

    A．      B．1     C．2     D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     函数f(x)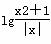＝ (x≠0，x∈R)，有下列命题：

    ①f(x)的图象关于y轴对称；

    ②f(x)的最小值是2；

    ③f(x)在(－∞，0)上是减函数，在(0，＋∞)上是增函数；

    ④f(x)没有最大值．

    其中正确命题的序号是________．(请填上所有正确命题的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设α为第四象限的角，若，则tan2α=        .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若Sn和Tn分别表示数列{an}和{bn}的前n项和，对任意正整数an=-2(n+1),Tn-3S­=4n.

    (Ⅰ)求数列{bn}的通项公式；

    （Ⅱ）在平面直角坐标系内，直线ln的斜率为bn.且与曲线y=x2有且仅一个交点，与y轴交于Dn，记dn=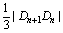-(2n+7)求dn;

    查看答案和解析>>

    同步练习册答案