
【题目】已知函数![]() ,
,![]() (e为自然对数的底数,e≈2.718).对于任意的
(e为自然对数的底数,e≈2.718).对于任意的![]() (0,e),在区间(0,e)上总存在两个不同的
(0,e),在区间(0,e)上总存在两个不同的![]() ,
,![]() ,使得
,使得![]() =
=![]() =
=![]() ,则整数a的取值集合是_______.
,则整数a的取值集合是_______.
【答案】![]()
【解析】
根据函数的单调性求出f(x)的值域,求出g(x)的单调性,问题转化为关于a的不等式组,求出a的范围即可.
f′(x)=2(![]() ﹣x),
﹣x),
令f′(x)>0,解得:0<x<![]() ,
,
令f′(x)<0,解得:![]() <x<e,
<x<e,
故f(x)在(0,![]() )递增,在(
)递增,在(![]() ,e)递减,
,e)递减,
而f(0)=0,f(![]() )=2,f(e)=e(2
)=2,f(e)=e(2![]() ﹣e),
﹣e),
故f(x)在(0,e)的值域是(0,2),
对于g(x)=lnx﹣ax+5,x∈(0,e),
a=0时,g(x)=lnx+5,g(x)递增,
在区间(0,e)上不存在两个不同的x1,x2,使得g(x1)=g(x2),
不合题意,
a≠0时,g′(x)=![]() ﹣a,令g′(x)=0,解得:x=
﹣a,令g′(x)=0,解得:x=![]() ,
,
若在区间(0,e)上总存在两个不同的x1,x2,使得g(x1)=g(x2),
则只需0<![]() <e,故a>
<e,故a>![]() ,
,
令g′(x)>0,解得:0<x<![]() ,令g′(x)<0,解得:
,令g′(x)<0,解得:![]() <x<e,
<x<e,
故g(x)在(0,![]() )递增,在(
)递增,在(![]() ,e)递减,
,e)递减,
而x→0时,g(x)→﹣∞,g(![]() )=﹣lna+4,g(e)=6﹣ae,
)=﹣lna+4,g(e)=6﹣ae,
若对于任意的x0∈(0,e),在区间(0,e)上总存在两个不同的x1,x2,
使得g(x1)=g(x2)=f(x0),
只需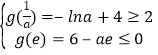 ,解得:2.2≈
,解得:2.2≈![]() ≤a≤e2≈7.29,
≤a≤e2≈7.29,
故满足条件的a的整数为:3,4,5,6,7,
故答案为:{3,4,5,6,7}.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,已知定点![]() ,点P是圆
,点P是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 相交于点
相交于点![]() .
.

(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)过定点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 的轨迹交于
的轨迹交于![]()
![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 中心为O,点E是侧棱
中心为O,点E是侧棱![]() 上的一个动点,有下列判断,正确的是( )
上的一个动点,有下列判断,正确的是( )

A.直三棱柱侧面积是![]() B.直三棱柱体积是
B.直三棱柱体积是![]()
C.三棱锥![]() 的体积为定值D.
的体积为定值D.![]() 的最小值为
的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a>0且a≠1).
(a>0且a≠1).
(1)若f(x)为定义域上的增函数,求实数a的取值范围;
(2)令a=e,设函数![]() ,且g(x1)+g(x2)=0,求证:x1+x2≥2+
,且g(x1)+g(x2)=0,求证:x1+x2≥2+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月![]() ,
,![]() 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中
两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中![]() ,
,![]() 两种支付方式都不使用的有5人,样本中仅使用
两种支付方式都不使用的有5人,样本中仅使用![]() 和仅使用
和仅使用![]() 的学生的支付金额分布情况如下:
的学生的支付金额分布情况如下:
交付金额(元) 支付方式 |
|
| 大于2000 |
仅使用 | 18人 | 9人 | 3人 |
仅使用 | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月![]() ,
,![]() 两种支付方式都使用的概率;
两种支付方式都使用的概率;
(Ⅱ)从样本仅使用![]() 和仅使用
和仅使用![]() 的学生中各随机抽取1人,以
的学生中各随机抽取1人,以![]() 表示这2人中上个月支付金额大于1000元的人数,求
表示这2人中上个月支付金额大于1000元的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,海岛O上有一座海拔300m的山,山顶上设有一个观察站A.上午11时测得一轮船在岛北偏东![]() 的B处,俯角为
的B处,俯角为![]() ;11时20分又测得该船在岛的北偏西
;11时20分又测得该船在岛的北偏西![]() 的C处,俯角为
的C处,俯角为![]() .
.

(1)该船的速度为每小时多少千米?
(2)若此船以不变的航速继续前进,则它何时到达岛的正西方向?此时船离开岛多少千米?(精确到lm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com