练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知定点，点P是圆上任意一点，线段的垂直平分线与半径相交于点.

    （1）当点在圆上运动时，求点的轨迹方程；

    （2）过定点且斜率为的直线与的轨迹交于两点，若，求点到直线的距离.

    【答案】（1）；（2）.

    【解析】

    （1）直接利用椭圆的定义式可知，，故而，此时，则根据可知，，则椭圆方程可求；

    （2）设出直线为：，与的轨迹方程联立，得出根与系数的关系，代入向量乘积表达式，求出，从而得出直线方程，则到直线的距离可求.

    （1）连接MD.由已知，得，由，

    ∴根据椭圆的定义，

    点M的轨迹是以C，D为焦点，长轴长为6的椭圆.

    ∴，，.

    ∴，点M的轨迹方程为.

    （2）由题设知直线l的方程为，代入M的轨迹方程，

    整理，得.

    设，.

    ∴，.

    ∵

    .

    ∴，解得.

    ∴点O到直线l的距离.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知f(x)＝x2＋2xtanθ－1，x∈[－1，]，其中θ∈(－，)．

    (1)当θ＝－时，求函数f(x)的最大值；

    (2)求θ的取值范围，使y＝f(x)在区间[－1，]上是单调函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）当时，求的极大值；

    （Ⅱ）若函数的极小值大于零，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了解高三复习效果，从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩，分成6组制成频率分布直方图如图所示：

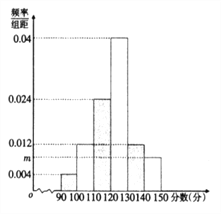
    （1）求的值及这50名同学数学成绩的平均数；

    （2）该学校为制定下阶段的复习计划，从成绩在的同学中选出3位作为代表进行座谈，若已知成在的同学中男女比例为2：1，求至少有一名女生参加座谈的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn，a1＝3，且Sn＝nan＋1－n2－n．

    （1）求{an}的通项公式；

    （2）若数列{bn}满足，求{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】A，B，C，D是空间不共面的四点，它们到平面a的距离之比依次为1：1：1：2，则满足条件的平面a的个数是：

    A. 1 B. 4 C. 7 D. 8.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义在区间D上的函数，若存在正整数k，使不等式恒成立，则称为型函数.

    （1）设函数，定义域.若是型函数，求实数a的取值范围；

    （2）设函数，定义域.判断是否为型函数，并给出证明.

    （参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某台函数计算器上有一个显示屏和两个操作键．若按一下第一个操作键，则将原显示屏上的数变为（表示不超过实数x的最大整数）；若按一下第二个操作键，则将原显示屏上的数变为．称按一下任意一个操作键为一次操作．现在显示屏上的数为1．问：

    （1）是否可以经过有限次操作，显示屏上出现整数2000？说明理由．

    （2）小于2000的整数中有多少个数可以经过有限次操作在显示屏上出现？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，（e为自然对数的底数，e≈2.718）．对于任意的(0，e)，在区间(0，e)上总存在两个不同的，，使得＝＝，则整数a的取值集合是_______．

    查看答案和解析>>

    同步练习册答案