
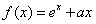 ,
,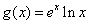 .(其中
.(其中 为自然对数的底数).
为自然对数的底数).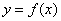 在
在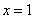 处的切线与直线
处的切线与直线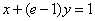 垂直,求
垂直,求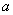 的值;
的值;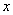 ≥0,
≥0,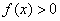 恒成立,试确定实数
恒成立,试确定实数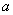 的取值范围;
的取值范围;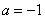 时,是否存在实数
时,是否存在实数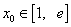 ,使曲线C:
,使曲线C: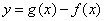 在点
在点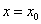 处的切线与
处的切线与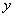 轴垂直?若存在,求出
轴垂直?若存在,求出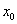 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 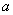 =-1 (2)
=-1 (2)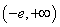 (3)不存在
(3)不存在 , 因此
, 因此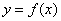 在
在 处的切线
处的切线 的斜率为
的斜率为 ,
,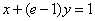 的斜率为
的斜率为 , ∴(
, ∴( )
) =-1,∴
=-1,∴ 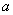 =-1.
=-1. ≥0时,
≥0时,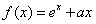
 恒成立,
恒成立, =0,此时,
=0,此时, ,
,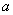 可为任意实数;
可为任意实数;  >0时,
>0时,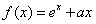
 恒成立,
恒成立, 恒成立, 设
恒成立, 设 =
=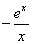 ,则
,则 =
=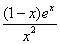 ,
, ∈(0,1)时,
∈(0,1)时, >0,
>0, 在(0,1)上单调递增,
在(0,1)上单调递增, ∈(1,+∞)时,
∈(1,+∞)时, <0,
<0, 在(1,+∞)上单调递减,
在(1,+∞)上单调递减, =1时,
=1时, 取得极大值,
取得极大值, , ∴ 实数
, ∴ 实数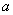 的取值范围为
的取值范围为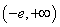 .
.  ,
,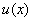 =
= ,则
,则
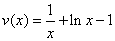 ,则
,则 ,
,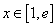 ,
, ,故
,故 在
在 上的最小值为
上的最小值为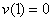 ,
,  ≥0,又
≥0,又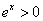 ,∴
,∴ >0,
>0,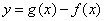 在点
在点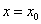 处的切线与
处的切线与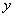 轴垂直,则
轴垂直,则 =0,矛盾。
=0,矛盾。 ,使曲线C:
,使曲线C: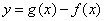 在点
在点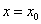 处的切线与
处的切线与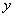 轴垂
轴垂

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com