
| A. | 有最大项无最小项 | B. | 有最小项无最大项 | ||
| C. | 既有最大项又有最小项 | D. | 无最大项也无最小项 |
分析 利用对数的运算性质化简f(x),代入化简f(2${\;}^{{a}_{n}}$)=2n,由一元二次方程的解法和0<2an<1,求出an,化简an+1判断出an+1>an,可得{an}单调递增,由单调性可得答案.
解答 解:由题意得,f(x)=log2x-logx2=log2x-$\frac{1}{lo{g}_{2}^{x}}$,
∴f(2${\;}^{{a}_{n}}$)=${log}_{2}^{{2}^{{a}_{n}}}-\frac{1}{lo{g}_{2}^{{2}^{{a}_{n}}}}$=2n,
则${a}_{n}-\frac{1}{{a}_{n}}=2n$,即an2-2nan-1=0,解得an=$n±\sqrt{{n}^{2}+1}$,
又0<2an<1,则an<0,即an=$n-\sqrt{{n}^{2}+1}$=$-\frac{1}{n+\sqrt{{n}^{2}+1}}$,
∴an+1=$-\frac{1}{n+1+\sqrt{({n+1)}^{2}+1}}$>an,
即an+1>an,则{an}单调递增,
∴数列{an}没有最大项但有最小项,
故选B.
点评 本题考查了数列的通项公式、单调性、对数的运算性质、一元二次方程的解法,考查了推理能力与计算能力,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
 如图,矩形ABEF所在的平面与等边△ABC所在的平面垂直,AB=2,AF=1,O为AB的中点.
如图,矩形ABEF所在的平面与等边△ABC所在的平面垂直,AB=2,AF=1,O为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,弦AB与CD相交于圆O内一点E,过E作BC的平行线与AD的延长线交于点P,且PD=2DA.
如图,弦AB与CD相交于圆O内一点E,过E作BC的平行线与AD的延长线交于点P,且PD=2DA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
| 支持“生育二胎” | a=3 | c=29 | 32 |
| 不支持“生育二胎” | b=7 | d=11 | 18 |
| 合计 | 10 | 40 | n=50 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 网友 | 强烈关注 | 一般关注 | 合计 |
| 重庆市 | a= | b= | |
| 四川省 | c= | d= | |
| 合计 |
| P(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
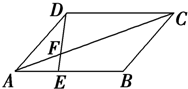
| A. | 16 cm2 | B. | 18 cm2 | C. | 20 cm2 | D. | 22 cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知c>0,设命题p:函数 为减函数.命题q:当
为减函数.命题q:当 时,函数f(x)=x+
时,函数f(x)=x+ >
> 恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com