
分析 利用双曲线的渐近线与直线l:3x+y+1=0垂直,求出a,然后求解双曲线的截距即可.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一条渐近线为:y=$\frac{1}{a}x$,
双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一条渐近线与直线l:3x+y+1=0垂直,可得:$-3×\frac{1}{a}$=-1,a=3.
所求双曲线的焦距为:2c=2$\sqrt{1+{a}^{2}}$=2$\sqrt{10}$.
故答案为:2$\sqrt{10}$.
点评 本题考查双曲线的渐近线方程的应用,双曲线的简单性质,考查计算能力.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
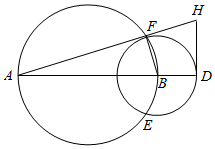 如图,A,B,D三点共线,以AB为直径的圆与以BD为半径的圆交于E,F,DH切圆B于点D,DH交AF于H.
如图,A,B,D三点共线,以AB为直径的圆与以BD为半径的圆交于E,F,DH切圆B于点D,DH交AF于H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理 | 化学 | 生物 | 信息技术 | |
| 周二 | $\frac{3}{4}$ | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{1}{4}$ |
| 周四 | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{2}$ |
| 周五 | $\frac{2}{3}$ | $\frac{1}{3}$ | $\frac{1}{4}$ | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 原油(%) | 天然气(%) | 原煤(%) | 核能(%) | 水力发电(%) | 再生能源(%) | |
| 2011年 | 17.7 | 4.5 | 70.4 | 0.7 | 6.0 | 0.7 |
| 2014年 | 17.5 | 5.6 | 66.0 | 1.0 | 8.1 | 1.8 |
| A. | 天然气 | B. | 核能 | C. | 水力发电 | D. | 再生能源 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com