
| ���� | ��ѧ | ���� | ��Ϣ���� | |
| �ܶ� | $\frac{3}{4}$ | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{1}{4}$ |
| ���� | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{2}$ |
| ���� | $\frac{2}{3}$ | $\frac{1}{3}$ | $\frac{1}{4}$ | $\frac{1}{3}$ |
���� ���������������������ܶ������ġ����嶼������Ϊ�¼�A������������ö����¼����ʼ��㹫ʽ��������������������ܶ������ġ����嶼�������ĸ��ʣ�
����X�Ŀ���ȡֵΪ0��1��2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ�������������X�ķֲ��к�EX��
��� �⣺���������������������ܶ������ġ����嶼������Ϊ�¼�A��
������ã�
���������������ܶ������ġ����嶼�������ĸ��ʣ�
P��A��=��1-$\frac{3}{4}$������1-$\frac{1}{2}$������1-$\frac{2}{3}$��=$\frac{1}{24}$��
����X�Ŀ���ȡֵΪ0��1��2��3��4��
P��X=0��=$��1-\frac{1}{2}��^{3}����1-\frac{1}{4}��$=$\frac{3}{32}$��
P��X=1��=${C}_{3}^{1}��\frac{1}{2}����1-\frac{1}{2}��^{2}����1-\frac{1}{4}��$+$\frac{1}{4}����1-\frac{1}{2}��^{3}$=$\frac{6}{15}$��
P��X=2��=${C}_{3}^{2}����\frac{1}{2}��^{2}��1-\frac{1}{2}������1-\frac{1}{4}��$+${C}_{3}^{1}��\frac{1}{2}����1-\frac{1}{2}��^{2}��\frac{1}{4}$=$\frac{3}{8}$��
P��X=3��=$��\frac{1}{2}��^{3}����1-\frac{1}{4}��+{C}_{3}^{2}����\frac{1}{2}��^{2}$��$��1-\frac{1}{2}����\frac{1}{4}$=$\frac{3}{16}$��
P��X=4��=$��\frac{1}{2}��^{3}��\frac{1}{4}$=$\frac{1}{32}$��
���������X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{3}{32}$ | $\frac{5}{16}$ | $\frac{3}{8}$ | $\frac{3}{16}$ | $\frac{1}{32}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��������¼����ʳ˷���ʽ�������¼����ʼ��㹫ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����x0�ʣ�-�ޣ�1]��ʹx${\;}_{0}^{3}$��${x}_{0}^{\frac{1}{3}}$ | B�� | ����x0�ʣ�1��+�ޣ���ʹx${\;}_{0}^{3}$��${x}_{0}^{\frac{1}{3}}$ | ||
| C�� | ����x0�ʣ�-�ޣ�1]��ʹx${\;}_{0}^{3}$��${x}_{0}^{\frac{1}{3}}$ | D�� | ����x0�ʣ�1��+�ޣ���ʹx${\;}_{0}^{3}$��${x}_{0}^{\frac{1}{3}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-10��0�� | B�� | ��-8��1�� | C�� | ��0��10�� | D�� | ��1��12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�$\frac{3}{2}$] | B�� | ��-�ޣ�1] | C�� | ��-1��$\frac{3}{2}$] | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -27 | B�� | 27 | C�� | ��27 | D�� | ��81 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� | 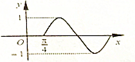 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O����ABΪֱ����Բ����C��Բ�ϣ��ڡ�ABC�͡�ACD�У���ADC=90�㣬��BAC=��CAD��DC���ӳ�����AB���ӳ��߽��ڵ�E����EB=6��EC=6$\sqrt{2}$����BC�ij�Ϊ2$\sqrt{3}$��
��ͼ����O����ABΪֱ����Բ����C��Բ�ϣ��ڡ�ABC�͡�ACD�У���ADC=90�㣬��BAC=��CAD��DC���ӳ�����AB���ӳ��߽��ڵ�E����EB=6��EC=6$\sqrt{2}$����BC�ij�Ϊ2$\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com