
分析 根据向量的坐标运算求出$\overrightarrow{CB}$,再根据直角△ABC中,B=$\frac{π}{2}$,得到$\overrightarrow{AB}$•$\overrightarrow{CB}$=2+1-k=0,解得即可.
解答 解:∵$\overrightarrow{AB}$=(2,1),$\overrightarrow{AC}$=(1,k),
∴$\overrightarrow{CB}$=$\overrightarrow{AB}$-$\overrightarrow{AC}$=(2,1)-(1,k)=(1,1-k),
∵B=$\frac{π}{2}$,
∴$\overrightarrow{AB}$⊥$\overrightarrow{CB}$,
∴$\overrightarrow{AB}$•$\overrightarrow{CB}$=2+1-k=0,
∴k=3,
故答案为:3
点评 本题考查了向量的加减的几何意义和向量的垂直的条件,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
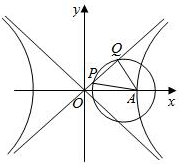 如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线C的渐近线方程为( )
如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{{\sqrt{3}}}{3}$x | B. | y=±$\frac{{\sqrt{3}}}{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{2\sqrt{3}}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6$\sqrt{2}$,则BC的长为2$\sqrt{3}$.
如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6$\sqrt{2}$,则BC的长为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 96种 | C. | 72种 | D. | 48种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com