
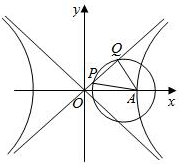
 如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线C的渐近线方程为( )
如图,已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{{\sqrt{3}}}{3}$x | B. | y=±$\frac{{\sqrt{3}}}{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{2\sqrt{3}}}{3}$x |
分析 设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,A(a,0),P(m,$\frac{bm}{a}$),(m>0),由向量共线的坐标表示,可得Q的坐标,求得弦长|PQ|,运用中点坐标公式,可得PQ的中点坐标,由两直线垂直的条件:斜率之积为-1,可得m=$\frac{{a}^{3}}{2{c}^{2}}$,半径r=$\frac{{a}^{2}}{c}$,运用圆的弦长公式计算即可得到a,b的关系,进而求得渐近线方程..
解答 解:设双曲线的一条渐近线方程为y=$\frac{b}{a}$x,A(a,0),
P(m,$\frac{bm}{a}$),(m>0),由$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,可得Q(3m,$\frac{3bm}{a}$),
圆的半径为r=|PQ|=$\sqrt{4{m}^{2}+\frac{4{b}^{2}{m}^{2}}{{a}^{2}}}$=2m•$\frac{c}{a}$,
PQ的中点为H(2m,$\frac{2bm}{a}$),
由AH⊥PQ,可得$\frac{2bm}{a(2m-a)}$=-$\frac{a}{b}$,
解得m=$\frac{{a}^{3}}{2{c}^{2}}$,r=$\frac{{a}^{2}}{c}$.
A到渐近线的距离为d=$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$,
则|PQ|=2$\sqrt{{r}^{2}-{d}^{2}}$=r,
即为d=$\frac{\sqrt{3}}{2}$r,即有$\frac{ab}{c}$=$\frac{\sqrt{3}}{2}$•$\frac{{a}^{2}}{c}$.
可得$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$.
即有渐近线的方程为y=±$\frac{\sqrt{3}}{2}$x.
故选:B.
点评 本题考查双曲线的渐近线方程的求法,注意运用中点坐标公式和两直线垂直的条件:斜率之积为-1,以及圆的弦长公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 原油(%) | 天然气(%) | 原煤(%) | 核能(%) | 水力发电(%) | 再生能源(%) | |
| 2011年 | 17.7 | 4.5 | 70.4 | 0.7 | 6.0 | 0.7 |
| 2014年 | 17.5 | 5.6 | 66.0 | 1.0 | 8.1 | 1.8 |
| A. | 天然气 | B. | 核能 | C. | 水力发电 | D. | 再生能源 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com