
分析 由条件利用相互独立事件的概率乘法公式,求得7abc=15[(b-1)(c-1)+(a-1)(c-1)+(a-1)(b-1)],不妨设5能整除c,求得c=5,再根据3能整除ab,不妨设3能整除b,分类讨论求得b的值,可得a的值,从而求得 甲、乙、丙三人都未解出此题的概率为(1-$\frac{1}{a}$)(1-$\frac{1}{b}$)(1-$\frac{1}{c}$)的值.
解答 解:由题意可得$\frac{1}{a}$(1-$\frac{1}{b}$)(1-$\frac{1}{c}$)+$\frac{1}{b}$(1-$\frac{1}{a}$)(1-$\frac{1}{c}$)+$\frac{1}{c}$(1-$\frac{1}{b}$)(1-$\frac{1}{a}$)=$\frac{7}{15}$,
即 $\frac{(b-1)(c-1)+(a-1)(c-1)+(a-1)(b-1)}{abc}$=$\frac{7}{15}$,即 7abc=15[(b-1)(c-1)+(a-1)(c-1)+(a-1)(b-1)],
故5能整除abc,不妨设5能整除c,由a、b、c都是小于10的正整数,可得c=5.
∴3[4(b-1)+4(a-1)+(a-1)(b-1)]=7ab,故3能整除ab,不妨设3能整除b,
则b=3,6,9.
若b=3,则a=2;若b=6,则3a+11=8a,a无整数解;若b=9,则3a+20=12a,a无整数解.
综上可得,a=2,b=3,c=5,
∴甲、乙、丙三人都未解出此题的概率为(1-$\frac{1}{a}$)(1-$\frac{1}{b}$)(1-$\frac{1}{c}$)=$\frac{(a-1)(b-1)(c-1)}{abc}$=$\frac{4}{15}$,
故答案为:$\frac{4}{15}$.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| 原油(%) | 天然气(%) | 原煤(%) | 核能(%) | 水力发电(%) | 再生能源(%) | |
| 2011年 | 17.7 | 4.5 | 70.4 | 0.7 | 6.0 | 0.7 |
| 2014年 | 17.5 | 5.6 | 66.0 | 1.0 | 8.1 | 1.8 |
| A. | 天然气 | B. | 核能 | C. | 水力发电 | D. | 再生能源 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
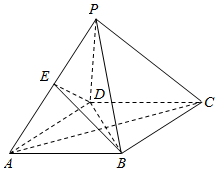 如图,四棱锥P-ABCD中,底面ABCD的边长为4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.
如图,四棱锥P-ABCD中,底面ABCD的边长为4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com