
分析 根据求导公式和法则求出f′(x),由条件转化为:x=0是方程f′(x)=0唯一的实根,对方程化简后转化为一元二次方程根的个数问题,利用判别式列出不等式,求出a的取值范围.
解答 解:由题意得f′(x)=4x3+ax2+$\frac{1}{8}$ax,
∵x=0是函数f(x)唯一的极值点,∴x=0是方程f′(x)=0唯一的实根,
由f′(x)=0得:x(4x2+ax+$\frac{1}{8}$a)=0,
∴方程4x2+ax+$\frac{1}{8}$a=0有唯一的根0或没有实根,
∴a=0或△=${a}^{2}-4×4×\frac{1}{8}a<$0,
解得0≤a<2,
∴实数a的取值范围是[0,2).
故答案为:[0,2)
点评 本题考查了利用导数研究函数的极值问题,考查了转化思想和分析问题能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
 如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6$\sqrt{2}$,则BC的长为2$\sqrt{3}$.
如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6$\sqrt{2}$,则BC的长为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn最大值为91 | B. | Sn最小值为91 | C. | Sn最大值为87 | D. | Sn最小值为87 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
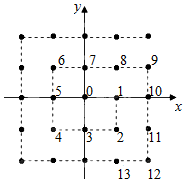 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如图规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,经归纳可知标注2013的格点的坐标为( )
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如图规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,经归纳可知标注2013的格点的坐标为( )| A. | (11,22) | B. | (12,23) | C. | (23,23) | D. | (23,22) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{7π}{12}$个单位得到 | B. | 向右平移$\frac{7π}{12}$个单位得到 | ||
| C. | 向左平移$\frac{7π}{24}$个单位得到 | D. | 向右平移$\frac{7π}{24}$个单位得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com