
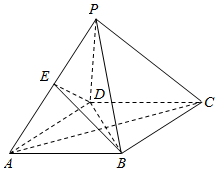
 如图,四棱锥P-ABCD中,底面ABCD的边长为4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.
如图,四棱锥P-ABCD中,底面ABCD的边长为4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.分析 (1)设AC∩BD=O,连结PO,推导出AC⊥BD,PO⊥BD,由此能证明BD⊥平面PAC.
(2)推导出PO⊥平面ABCD,求出S△ABC和PO,取AO中点F,连结EF,EF是△PAO中位线,从而EF⊥平面ABC,由此能求出三棱锥E-ABC的体积.
解答 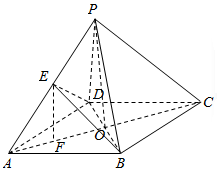 证明:(1)设AC∩BD=O,连结PO
证明:(1)设AC∩BD=O,连结PO
∵四棱锥P-ABCD中,底面ABCD的边长为4的菱形,
∴AC⊥BD,
∵PD=PB=4,∴PO⊥BD,
∵AC∩PO=O,∴BD⊥平面PAC.
解:(2)∵PA=PC,∴PO⊥AC,
又PO⊥BD,AC∩BD=O,
∴PO⊥平面ABCD,
∵底面ABCD的边长为4的菱形,PD=PB=4,∠BAD=60°,
∴BO=$\frac{1}{2}BD=\frac{1}{2}AB=2$,AC=2AO=2$\sqrt{A{B}^{2}-B{O}^{2}}$=2$\sqrt{16-4}$=4$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}×AC×BO=\frac{1}{2}×4\sqrt{3}×2$=$4\sqrt{3}$,
PO=$\sqrt{P{B}^{2}-B{O}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
取AO中点F,连结EF,
∵E是PA中点,∴EF是△PAO中位线,
∴EF∥PO,且EF=$\frac{1}{2}PO$=$\sqrt{3}$,
∴三棱锥E-ABC的体积VE-ABC=$\frac{1}{3}×{S}_{△ABC}×EF$=$\frac{1}{3}×4\sqrt{3}×\sqrt{3}$=4.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -27 | B. | 27 | C. | ±27 | D. | ±81 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6$\sqrt{2}$,则BC的长为2$\sqrt{3}$.
如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6$\sqrt{2}$,则BC的长为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
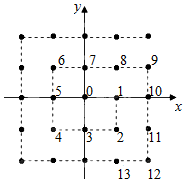 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如图规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,经归纳可知标注2013的格点的坐标为( )
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如图规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,经归纳可知标注2013的格点的坐标为( )| A. | (11,22) | B. | (12,23) | C. | (23,23) | D. | (23,22) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com