
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用指数函数过定点(0,1),得到函数y=1+logmx(m>0且m≠1)的图象恒过点M(1,1),由此得到关于a,b的等式,利用基本不等式求最小值.
解答 解:由已知得到指数函数过定点(0,1),得到函数y=1+logmx(m>0且m≠1)的图象恒过点M(1,1),又直线$\frac{x}{a}+\frac{y}{b}=1$(a>0,b>0)经过点M,
所以$\frac{1}{a}+\frac{1}{b}$=1,所以(a+b)($\frac{1}{a}+\frac{1}{b}$)=2+$\frac{b}{a}+\frac{a}{b}$≥2$+2\sqrt{\frac{b}{a}•\frac{a}{b}}$=4;
当且仅当a=b时等号成立;
故选:C.
点评 本题考查了指数函数的图象以及利用基本不等式求最小值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | (-2,0] | C. | (-2,0) | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
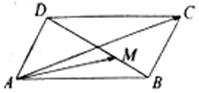 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{4})$ | B. | $(-\frac{1}{4},+∞)$ | C. | (0,+∞) | D. | (-∞,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com