
梯形的两腰和一底如果相等,它的对角线必平分另一底上的两个角.
已知:在如图所示梯形ABCD中,AD∥BC,AB=DC=AD,AC和BD是它的对角线.
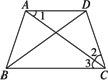
求证:AC平分∠BCD,BD平分∠CBA.
|
证明:(1)等腰三角形两底角相等,(大前提) △DAC是等腰三角形,DA、DC为两腰,(小前提) ∴∠1=∠2.(结论) (2)两条平行线被第三条直线截出的内错角相等,(大前提) ∠1和∠3是平行线AD、BC被AC截出的内错角,(小前提) ∴∠1=∠3.(结论) (3)等于同一个量的两个量相等,(大前提) ∠2和∠3都等于∠1,(小前提) ∴∠2=∠3.(结论)即AC平分∠BCD. (4)同理DB平分∠CBA. 思路分析:本题可由三段论逐步推理论证. |
|
命题的推理证明为多个三段论,称为复合三段论.事实上,每一次三段论的大前提可不写出,某一次三段论的小前提如果是它前面某次三段论的结论,也可不再写出,即过程可简写. |


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:同步题 题型:证明题
查看答案和解析>>
科目:高中数学 来源: 题型:
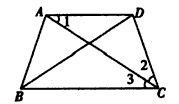
已知在梯形ABCD中(如图2-1-11),AB=DC=AD,AC和BD是它的对角线,求证:AC平分∠BCD,DB平分∠CBA.

图2-1-11
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在梯形ABCD中(如图2-1-11),AB=DC=AD,AC和BD是它的对角线,求证:AC平分∠BCD,DB平分∠CBA.
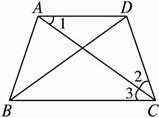
图2-1-11
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在如图所示的梯形ABCD中,AD∥BC,AD=DC=AD,AC和BD是它的对角线.
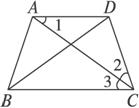
求证:AC平分∠BCD,BD平分∠CBA.
分析:本题可由三段论逐步推理论证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com