
分析 (1)利用二次函数的奇偶性求出m,然后通过f(2)=2求解n,得到函数的解析式.
(2)化简函数的解析式,利用函数的单调区间求解b的范围即可.
解答 解:(1)f(x)=x2+mx-n为偶函数,可得m=0,因为f(2)=2,
所以2=4-n,解得n=2.
函数的解析式为:f(x)=x2-2.
(2)h(x)=f(x)-(b+1)x=x2-(b+1)x-2在(-1,2)上是单调函数,
可知函数的对称轴为:x=$\frac{b+1}{2}$,
满足:$\frac{b+1}{2}≤-1$或$\frac{b+1}{2}≥2$,
解得b≤-3或b≥3.
b的取值范围:(-∞,-3]∪[3,+∞).
点评 本题考查二次函数的简单性质的应用,注意二次函数的开口方向以及对称轴与函数的单调性的关系.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{3}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>y则x>|y|”的逆命题 | |
| B. | 命题“若x=1,则x2+x-2=0”的否命题 | |
| C. | 命题“若x>1,则x2>1”的否命题 | |
| D. | 命题“若x2>0,则函数x>1”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {-2,3} | C. | {(2,3)} | D. | {(-2,3)} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3.
在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,∠A=120°,BD=3.查看答案和解析>>
科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
如图, 在四棱锥 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形,
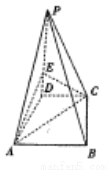
(1)在 上确定一点
上确定一点 ,使得
,使得 平面
平面 ,并求
,并求 的值;
的值;
(2)在(1)条件下, 求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com