
分析 (1)欲求曲线y=f(x)在点(1,f(1))处的切线方程只需求出切线斜率k=f′(1),从而求出切线方程;
(2)求出 f′(x)=ex-1(x+1)-mx-m=(x+1)(ex-1-m),通过讨论m的范围,求出函数的单调区间,从而求出函数的极值即可;
分 ①当m≤0,②当m>0 讨论,求出函数的单调区间,从而求出函数的极值即可;
解答 解:(1)当m=0时,f(x)=xex-1,f′(x)=ex-1(x+1),
f′(1)=2,f(1)=1,
∴曲线y=f(x)在点(1,f(1))处的切线方程y-1=2(x-1),即2x-y-1=0
(2)f′(x)=ex-1(x+1)-mx-m=(x+1)(ex-1-m),
①当m≤0时,ex-1-m>0恒成立,当x>-1时,f′(x)>0,当x<-1时,f′(x)<0,
此时函数f(x)在(-∞,-1)单调递减,在(-1,+∞)单调递增,有极小值f(-1)=-e-2+$\frac{1}{2}m$.
②当m>0时,令f′(x)=ex-1(x+1)-mx-m=(x+1)(ex-1-m)=0,
可得1=-1,x2=lnm+1
当0<m<e-2时,x2<x1,
x∈(-∞,lnm+1)时,f′(x)>0,x∈(lnm+1,-1)时,f′(x)<0,x∈(-1,+∞)时,f′(x)>0,
此时,函数f(x)在(-∞,lnm+1),(-1,+∞)单调递增,在(lnm+1,-1)单调递减,
有极大值f(lnm+1)=-$\frac{1}{2}(lnm+1)^{2}$,有极小值f(-1)=-e-2+$\frac{1}{2}m$.;
当m=e-2时,函数f(x)在(-∞,+∞)单调递增,无极值;
当m>e-2时,x∈(-∞,-1)时,f′(x)>0,x∈(-1,lnm+1)时,f′(x)<0,x∈(lnm+1,+∞)时,f′(x)>0,
此时,函数f(x)在(-∞,-1),(lnm+1,+∞)单调递增,在(-1,lnm+1)单调递减,
有极小值f(lnm+1)=-$\frac{1}{2}(lnm+1)^{2}$,有极大值f(-1)=-e-2+$\frac{1}{2}m$.;
点评 本题考查了函数的单调性及函数的极值问题及导数的几何意义,考查了分类讨论思想,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
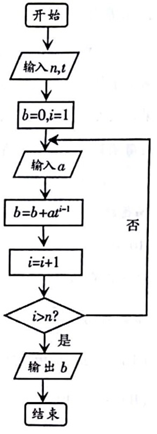 在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )
在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )| A. | 179 | B. | 178 | C. | 147 | D. | 146 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -e | B. | 2 | C. | -2 | D. | $\frac{1}{e}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com