
分析 (1)由两向量的坐标,利用平面向量数量积运算法则确定出f(x)解析式,找出ω的值,代入周期公式即可得到结果;
(2)根据f(x)的最小值为0,确定出m的值,进而确定出f(x)解析式,求出最大值,以及此时x的集合即可.
解答 解:(1)∵向量$\overrightarrow a$=(2sinx,cosx),$\overrightarrow b$=($\sqrt{3}$cosx,2cosx),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2$\sqrt{3}$sinxcosx+2cos2x,
∴f(x)=2$\sqrt{3}$sinxcosx+2cos2x+m=$\sqrt{3}$sin2x+cos2x+m+1=2sin(2x+$\frac{π}{6}$)+m+1,
∵ω=2,T=$\frac{2π}{2}$=π;
(2)f(x)min=-2+m+1=0,即m=1,
∴f(x)=2sin(2x+$\frac{π}{6}$)+2,f(x)max=2+2=4,
当2x+$\frac{π}{6}$=$\frac{π}{2}$+2kπ,k∈Z,即x=$\frac{π}{6}$+kπ,k∈Z时,函数f(x)取得最大值,
则函数f(x)取值最大值时,自变量x的集合为{x|x=$\frac{π}{6}$+kπ,k∈Z}.
点评 此题考查了平面向量的数量积的运算,三角函数的周期性及其求法,以及三角函数的最值,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | cardA=5 | B. | cardB=3 | C. | card(A∩B)=2 | D. | card(A∪B)=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,$\frac{π}{4}$) | B. | ($\sqrt{2}$,$\frac{7π}{4}$) | C. | (2,$\frac{π}{4}$) | D. | (2,$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
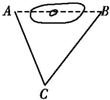 如图,为了测量A、B两点间的距离,在地面上选择适当的点C,测得AC=100m,BC=120m,∠ACB=60°,那么A、B的距离为( )
如图,为了测量A、B两点间的距离,在地面上选择适当的点C,测得AC=100m,BC=120m,∠ACB=60°,那么A、B的距离为( )| A. | 20$\sqrt{91}$ m | B. | 20$\sqrt{31}$ m | C. | 500 m | D. | 60$\sqrt{66}$ m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 中国鞋码实际标注(同国标码)mm | 220 | 225 | 230 | 235 | 240 | 245 | 250 | 255 | 260 | 265 |
| 中国鞋码习惯叫法(同欧码) | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com