
分析 由条件,结合对数函数的性质,可得0<a<1,运用作差法和对数的运算性质,结合基本不等式和对数函数的单调性,即可得证.
解答 证明:函数f(x)=loga(x+1)在区间(-1,+∞)上递减,
即有0<a<1,
对于任意实数x1>0,x2>0,
$\frac{1}{2}$[f(x1-1)+f(x2-1)]-f( $\frac{{x}_{1}{+x}_{2}}{2}$-1)
=$\frac{1}{2}$(logax1+logax2)-loga $\frac{{x}_{1}{+x}_{2}}{2}$
=loga $\sqrt{{{x}_{1}x}_{2}}$-loga $\frac{{x}_{1}{+x}_{2}}{2}$,
由于 $\frac{{x}_{1}{+x}_{2}}{2}$≥$\sqrt{{{x}_{1}x}_{2}}$,
又0<a<1,
则loga $\sqrt{{{x}_{1}x}_{2}}$≥loga $\frac{{x}_{1}{+x}_{2}}{2}$,
则有$\frac{1}{2}$[f(x1-1)+f(x2-1)]≥f( $\frac{{x}_{1}{+x}_{2}}{2}$-1),
当且仅当x1=x2取得等号.
点评 本题考查对数函数的单调性的运用,同时考查对数的运算性质,考查运算能力,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC一A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
如图,在三棱柱ABC一A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
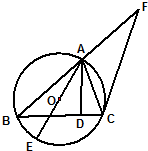 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
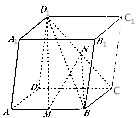 如图,在棱长为2的正方体ABCD-A1B1C1D1中,AB,D1C的中点分别是M,N
如图,在棱长为2的正方体ABCD-A1B1C1D1中,AB,D1C的中点分别是M,N查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | D⊆A | B. | D=B | C. | D⊆C | D. | D=C |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
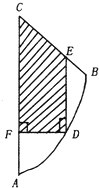 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com