
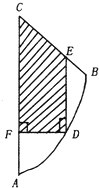
 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值. 分析 以AC所在的直线为y轴,A为坐标原点建立平面直角坐标系,求出曲边AB所在的抛物线方程;设出点D为(x,x2),表示出|DF|、|DE|与|CF|的长,求出直角梯形CEDF的面积表达式,利用导数求出它的最大值即可.
解答 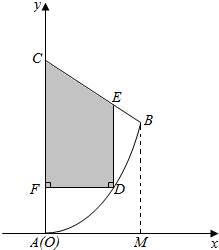 解:以AC所在的直线为y轴,A为坐标原点,
解:以AC所在的直线为y轴,A为坐标原点,
建立平面直角坐标系xOy,如图所示;
则A(0,0),C(0,8),
设曲边AB所在的抛物线方程为y=ax2(a>0),
则点B(2,4a),
又|BC|=$\sqrt{(4a-8)^{2}+{2}^{2}}$=2$\sqrt{5}$,
解得a=1或a=3(此时4a=12>8,不合题意,舍去);
∴抛物线方程为y=x2,x∈[0,2];
设点D(x,x2),则F(0,x2),
直线BC的方程为:2x+y-8=0,
∴E(x,8-2x),
|DF|=x,|DE|=8-2x-x2,|CF|=8-x2,
直角梯形CEDF的面积为:
S(x)=$\frac{1}{2}$x[(8-2x-x2)+(8-x2)]=-x3-x2+8x,x∈(0,2),
求导得S′(x)=-3x2-2x+8,
令S′(x)=0,解得x=$\frac{4}{3}$或x=-2(不合题意,舍去);
当x∈(0,$\frac{4}{3}$)时,S(x)单调递增,
x∈($\frac{4}{3}$,2)时,S(x)单调递减,
∴x=$\frac{4}{3}$时,S(x)取得最大值是
S($\frac{4}{3}$)=-($\frac{4}{3}$)3-$\frac{16}{9}$+8×$\frac{4}{3}$=$\frac{176}{27}$;
∴科技园区面积S的最大值为$\frac{176}{27}$.
点评 本题考查了函数与导数的综合应用问题,解题时要认真审题,仔细分析题设中的数量关系,合理地建立直角坐标系,利用导数求函数的最大值,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
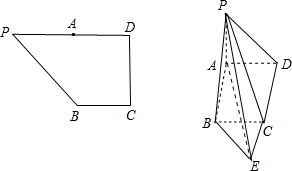 如图,在直角梯形PBCD中,∠D=∠C=90°,BC=CD=2,PD=4,A为PD的中点,将△PAB沿AB折起,使平面PAB⊥平面ABCD.
如图,在直角梯形PBCD中,∠D=∠C=90°,BC=CD=2,PD=4,A为PD的中点,将△PAB沿AB折起,使平面PAB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | $\frac{3\sqrt{2}}{2}$-1 | C. | $\frac{3\sqrt{3}}{2}$-1 | D. | 2$\sqrt{3}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
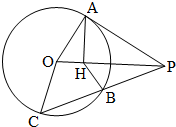 如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.
如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com