
分析 (Ⅰ)求出f(x)的导数,讨论m≤0时,m>0时,求得单调区间,可得最大值,解方程可得m的值;
(Ⅱ)求得函数y的解析式,由函数零点的定义,变形可得g(t)=$\frac{1-t}{1+t}$+lnt(t=$\frac{{x}_{2}}{{x}_{1}}$≥e).求出导数,判断单调性,可得最小值.
解答 解:(Ⅰ)f(x)的导数为f′(x)=$\frac{1}{x}$-m=$\frac{1-mx}{x}$,
m≤0时,f′(x)>0,f(x)在(0,+∞)单调递增,f(x)=lnx-mx在(0,+∞)无最大值.
m>0,易知当x∈(0,$\frac{1}{m}$)时,f′(x)>0,f(x)在(0,$\frac{1}{m}$)单调递增;
当x∈($\frac{1}{m}$,+∞)时,f′(x)<0,f(x)在($\frac{1}{m}$,+∞)单调递减,
故f(x)max=f($\frac{1}{m}$)=ln$\frac{1}{m}$-1=-1.即m=1.
综上可得m=1.
(Ⅱ)y=(x1-x2)f′(x1+x2)═(x1-x2)($\frac{1}{{x}_{1}+{x}_{2}}$-m)=$\frac{{x}_{1}-{x}_{2}}{{x}_{1}+{x}_{2}}$-m(x1-x2).
又$\left\{\begin{array}{l}{ln{x}_{1}-m{x}_{1}=0}\\{ln{x}_{2}-m{x}_{2}=0}\end{array}\right.$,故lnx1-lnx2=mx1-mx2,
即ln$\frac{{x}_{1}}{{x}_{2}}$=m(x1-x2).
故y=$\frac{{x}_{1}-{x}_{2}}{{x}_{1}+{x}_{2}}$-m(x1-x2)=$\frac{{x}_{1}-{x}_{2}}{{x}_{1}+{x}_{2}}$+ln$\frac{{x}_{2}}{{x}_{1}}$=$\frac{1-\frac{{x}_{2}}{{x}_{1}}}{1+\frac{{x}_{2}}{{x}_{1}}}$+ln$\frac{{x}_{2}}{{x}_{1}}$,
令g(t)=$\frac{1-t}{1+t}$+lnt(t=$\frac{{x}_{2}}{{x}_{1}}$≥e).
而g′(t)=$\frac{-2}{(1+t)^{2}}$+$\frac{1}{t}$=$\frac{1+{t}^{2}}{t(t+1)^{2}}$>0,
故g(t)在[e,+∞)单调递增.
故g(t)min=g(e)=$\frac{1-e}{1+e}$+1=$\frac{2}{1+e}$.
则y的最小值为$\frac{2}{1+e}$.
点评 本题考查导数的运用:求单调区间和极值、最值,考查函数零点的概念和运用,考查构造函数法和运用导数判断单调性及运用,考查化简整理的运算能力,属于中档题.


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
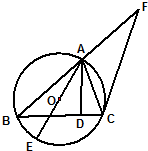 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
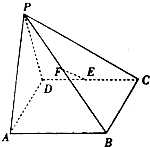 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD为等边三角形且平面PAD⊥底面ABCD,E、F分别为CD、PB的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD为等边三角形且平面PAD⊥底面ABCD,E、F分别为CD、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
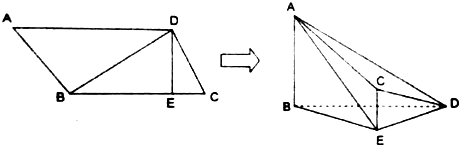
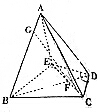 如图所示,在四棱锥A-BCDEE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE.又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDEE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE.又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
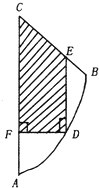 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
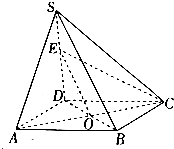 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,O是AC与BD的交点.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,O是AC与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com