
分析 (1)函数f(x)=log2(4x+1)-x是偶函数.利用对数性质能推导出f(-x)=f(x).
(2)根据偶函数在对称区间上单调性相反,可得f(x)的单调性;
(3)若f(m)-f(2m+1)<0,则f(m)<f(2m+1),结合函数的单调性,可得答案.
解答 解:(1)函数f(x)=log2(4x+1)-x是偶函数,理由如下:
函数f(x)=log2(4x+1)-x的定义域R关于原点对称,
且f(-x)=log2(4-x+1)+x=log2($\frac{{4}^{x}+1}{{4}^{x}}$)+x=log2(4x+1)-2x+x=log2(4x+1)-x=f(x),
故f(x)为偶函数;
(2)偶函数在对称区间上单调性相反,
故函数f(x)在(0,+∞)为增函数,在(-∞,0)上为减函数;
(3)若f(m)-f(2m+1)<0,则f(m)<f(2m+1),
则|m|<|2m+1|,即m2<(2m+1)2,
解得:m∈(-∞,-1)∪(-$\frac{1}{3}$,+∞)
点评 本题考查的知识是函数的奇偶性,函数的单调性,利用单调性解不等式,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx+x=1 | B. | sinx-x=1 | C. | x•sinx+x=1 | D. | x•sinx-x=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
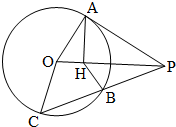 如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.
如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 5 | C. | $2\sqrt{3}+2$ | D. | $2\sqrt{2}+3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com