
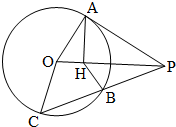
 如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.
如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.分析 (1)由射影定理知:PA2=PH•PO,根据切线长定理知:PA2=PB•PC,即可证明:△PHB~△PCO;
(2)求出S△OCP=$\frac{1}{2}×1×\sqrt{6}×\frac{\sqrt{10}}{4}$=$\frac{\sqrt{15}}{4}$.由△PHB∽△PCO,相似比为$\frac{PB}{PO}$=$\frac{\sqrt{6}}{4}$,面积比为($\frac{\sqrt{6}}{4}$)2=$\frac{3}{8}$,从而求出四边形BCOH的面积.
解答 证明:(1)在直角△POA中,由射影定理知:PA2=PH•PO,
又根据切线长定理知:PA2=PB•PC,
从而PH•PO=PB•PC,即$\frac{PH}{PC}=\frac{PB}{PO}$,
∵∠BPH=∠OPC,
∴△PHB~△PCO;
解:(2)由勾股定理PO=2,由切线长定理PA2=PB•PC,可得PC=$\sqrt{6}$,
在△POC中,cosC=$\frac{1+6-4}{2×1×\sqrt{6}}$=$\frac{\sqrt{6}}{4}$,
∴sinC=$\frac{\sqrt{10}}{4}$
所以S△OCP=$\frac{1}{2}×1×\sqrt{6}×\frac{\sqrt{10}}{4}$=$\frac{\sqrt{15}}{4}$.
由△PHB∽△PCO,相似比为$\frac{PB}{PO}$=$\frac{\sqrt{6}}{4}$,面积比为($\frac{\sqrt{6}}{4}$)2=$\frac{3}{8}$
从而四边形BCOH的面积S=$\frac{5}{8}$S△OCP=$\frac{5}{32}\sqrt{15}$.
点评 本题考查三角形相似的判定与性质,考查切线长定理、射影定理,考查学生分析解决问题的能力,属于中档题.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
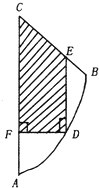 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到AC边的距离为2Km,另外两边AC、BC的长度分别为8Km,2$\sqrt{5}$Km.现欲在此地块内建一形状为直角梯形DECF的科技园区.求科技园区面积的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
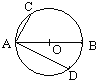 如图,已知AB是⊙O的直径,AB=2,AC和AD是⊙O的两条弦,AC=$\sqrt{2}$,AD=$\sqrt{3}$,则∠CAD的弧度数为75°.
如图,已知AB是⊙O的直径,AB=2,AC和AD是⊙O的两条弦,AC=$\sqrt{2}$,AD=$\sqrt{3}$,则∠CAD的弧度数为75°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com