
分析 (1)令a-ax>0,结合0<a<1可得函数的定义域,进而求出真数的范围,可得函数的值域;
(2)根据复合函数的单调性“同增异减”的原则,分析内外函数的单调性,可得绪论;
(3)求出函数的反函数,可将原不等式化为1<x2-2<x,解得答案.
解答 解:(1)令a-ax>0,则a>ax,
∵0<a<1,
∴x>1,
即函数的定义域为(1,+∞);
则t=a-ax∈(0,a),
故函数的值域为(1,+∞);
(2)∵0<a<1,
∴t=a-ax为增函数,
∴函数f(x)=loga(a-ax)为减函数,
(3)∵f(x)=loga(a-ax)
∴f-1(x)=loga(a-ax)
若f-1(x2-2)>f(x),
则1<x2-2<x,
解得:x∈($\sqrt{3}$,2)
点评 本题考查的知识点是复合函数的单调性,指数函数和对数函数的图象和性质,难度中档.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
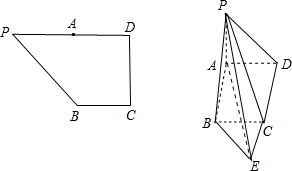 如图,在直角梯形PBCD中,∠D=∠C=90°,BC=CD=2,PD=4,A为PD的中点,将△PAB沿AB折起,使平面PAB⊥平面ABCD.
如图,在直角梯形PBCD中,∠D=∠C=90°,BC=CD=2,PD=4,A为PD的中点,将△PAB沿AB折起,使平面PAB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx+x=1 | B. | sinx-x=1 | C. | x•sinx+x=1 | D. | x•sinx-x=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
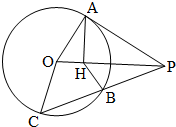 如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.
如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com