
分析 由二次根式的性质可得-1≤x≤1,然后由柯西不等式求解最大值即可.
解答 解:根据题意得:$\left\{\begin{array}{l}{x+1≥0}\\{1-x≥0}\end{array}\right.$,
解得:-1≤x≤1,
由柯西不等式得:y=$\sqrt{x+1}$+$\sqrt{1-x}$≤$\sqrt{{1}^{2}+{1}^{2}}$•$\sqrt{(\sqrt{x+1})^{2}+({\sqrt{1-x})}^{2}}$=2(当且仅当$\sqrt{x+1}$=$\sqrt{1-x}$,即x=0时,取等号),
故函数y=$\sqrt{x+1}$+$\sqrt{1-x}$的最大值为2.
故答案为:2.
点评 此题考查了无理函数的最值问题.此题难度适中,注意掌握柯西不等式的应用是解此题的关键,注意柯西不等式:ax+by≤$\sqrt{{a}^{2}+{b}^{2}}$•$\sqrt{{x}^{2}+{y}^{{\;}^{2}}}$(当且仅当ay=bx时取“=”).


科目:高中数学 来源: 题型:解答题
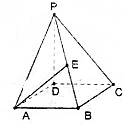 四棱锥P-ABCD中,底面是边长为6的菱形,且∠BAD=60°,PD⊥平面ABCD,PD=8.
四棱锥P-ABCD中,底面是边长为6的菱形,且∠BAD=60°,PD⊥平面ABCD,PD=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com