
分析 (1)由x=5时,y=11,代入函数的解析式,解关于a的方程,可得a值;
(2)商场每日销售该商品所获得的利润=每日的销售量×销售该商品的单利润,可得日销售量的利润函数为关于x的三次多项式函数,再用求导数的方法讨论函数的单调性,得出函数的极大值点,从而得出最大值对应的x值.
解答 解:(1)因为x=5时,y=11,
y=$\frac{a}{x-3}$+10(x-6)2,其中3<x<6,a为常数.
所以$\frac{a}{2}$+10=11,故a=2;
(2)由(1)可知,该商品每日的销售量y=$\frac{2}{x-3}$+10(x-6)2,
所以商场每日销售该商品所获得的利润为f(x)=(x-3)[$\frac{2}{x-3}$+10(x-6)2]
=2+10(x-3)(x-6)2,3<x<6.
从而,f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-6)(x-4),
于是,当x变化时,f(x)、f′(x)的变化情况如下表:
| x | (3,4) | 4 | (4,6) |
| f'(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值42 | 单调递减 |
点评 本题考查导数在实际问题中的运用:求最值,求出利润的函数式和正确求导是解题的关键,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
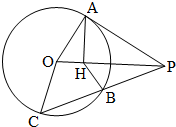 如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.
如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 5 | C. | $2\sqrt{3}+2$ | D. | $2\sqrt{2}+3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | 3 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com