
分析 (1)利用代入法求点M的轨迹方程,
(2)求出${λ^2}=\frac{{{x^2}+{y^2}}}{{{{(x-a)}^2}+{y^2}}}$=$\frac{{{x^2}+8-{{(x+2)}^2}}}{{{{(x-a)}^2}+8-{{(x+2)}^2}}}$=$\frac{4(1-x)}{{4+{a^2}-(2a+4)x}}$,可得结论;
(3)利用韦达定理及向量垂直的结论,即可求m的范围.
解答 解:(1)设点M(x,y),则H(2x+6,2y-3),
又H在圆上,得(2x+6-2)2+(2y-3+3)2=32,化简得(x+2)2+y2=8.
(2)设M的轨迹交y轴于E、F,由$\frac{{|{EO}|}}{{|{EA}|}}=\frac{{|{FO}|}}{{|{FA}|}}$且|EO|=|FO|知,|EA|=|FA|,
所以A在x轴上,设M(x,y),
则${λ^2}=\frac{{{x^2}+{y^2}}}{{{{(x-a)}^2}+{y^2}}}$=$\frac{{{x^2}+8-{{(x+2)}^2}}}{{{{(x-a)}^2}+8-{{(x+2)}^2}}}$=$\frac{4(1-x)}{{4+{a^2}-(2a+4)x}}$,
所以4+a2=2a+4,a=2或0(舍),即A(2,0),$λ=\frac{{\sqrt{2}}}{2}$;
(3)由$\left\{{\begin{array}{l}{y=kx}\\{{{(x+2)}^2}+{y^2}=8}\end{array}}\right.$消去y得(1+k2)x2+4x-4=0,
∴${x_1}+{x_2}=-\frac{4}{{1+{k^2}}}={x_1}{x_2}$,
又 0=$\overrightarrow{BN}•\overrightarrow{CN}=(1+{k^2}){x_1}{x_2}-km({x_1}+{x_2})+{m^2}$,
∴$0=-4+\frac{4km}{{1+{k^2}}}+{m^2}$即$\frac{{4-{m^2}}}{4m}=\frac{k}{{1+{k^2}}}∈[-\frac{1}{2},\frac{1}{2}]$
由$-\frac{1}{2}≤\frac{{4-{m^2}}}{4m}≤\frac{1}{2}得m∈[-\sqrt{5}-1,-\sqrt{5}+1]∪[\sqrt{5}-1,\sqrt{5}+1]$.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx+x=1 | B. | sinx-x=1 | C. | x•sinx+x=1 | D. | x•sinx-x=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
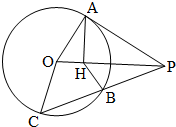 如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.
如图所示,设P为圆O外的点,过点P作圆O的切线PA,切点为A,过点P作圆O的割线PBC,与圆交于B,C两点,AH⊥OP,垂足为H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 5 | C. | $2\sqrt{3}+2$ | D. | $2\sqrt{2}+3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | 3 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 等边三角形 | D. | 直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com