
分析 (1)由对数式的真数大于0,然后求解三角不等式得答案;
(2)由根式内部的代数式大于等于0,然后求解三角不等式得答案;
(3)分别由对数式的真数大于0,根式内部的代数式大于等于0,求解三角不等式,再取交集得答案.
解答 解:(1)由sinx>0,得2kπ<x<π+2kπ,k∈Z.
∴函数y=lg(sinx)的定义域为(2kπ,π+2kπ),k∈Z;
(2)由1-2sin2x≥0,得-$\frac{\sqrt{2}}{2}≤sinx≤\frac{\sqrt{2}}{2}$,即$-\frac{π}{4}+kπ≤x≤\frac{π}{4}+kπ,k∈Z$.
∴y=$\sqrt{1-2si{n}^{2}x}$的定义域为[$-\frac{π}{4}+kπ,\frac{π}{4}+kπ$],k∈Z;
(3)由$\left\{\begin{array}{l}{2sinx-1>0①}\\{64-{x}^{2}≥0②}\end{array}\right.$,
解①得:$\frac{π}{6}+2kπ<x<\frac{5π}{6}+2kπ,k∈Z$;
解②得:-8≤x≤8.
①②取交集得:x∈$(-\frac{11π}{6},-\frac{7π}{6})∪(\frac{π}{6},\frac{5π}{6})∪(\frac{13π}{6},8]$.
∴y=lg(2sinx-1)+$\sqrt{64-{x}^{2}}$的定义域为$(-\frac{11π}{6},-\frac{7π}{6})∪(\frac{π}{6},\frac{5π}{6})∪(\frac{13π}{6},8]$.
点评 本题考查函数的定义域及其求法,考查了三角不等式的解法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
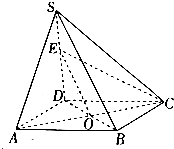 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,O是AC与BD的交点.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,O是AC与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com