
【题目】用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数
为偶函数
(1)求实数a的值;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣ ![]() ,判断λ与E的关系;
,判断λ与E的关系;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式2x2﹣x﹣3>0解集为( )
A.{x|﹣1<x< ![]() }??
}??
B.{x|x> ![]() 或x<﹣1}??
或x<﹣1}??
C.{x|﹣ ![]() <x<1}??
<x<1}??
D.{x|x>1或x<﹣ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布直方图. 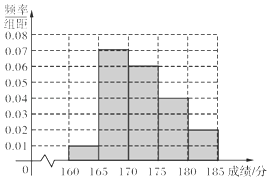
(1)为了能选拔出优秀的学生,该校决定在笔试成绩较高的第3组、第4组、第5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试;
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生由考官A面试,求第4组至少有一名学生被考官A面试的概.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com