
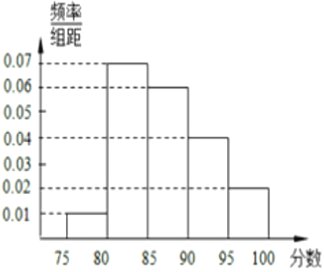
【题目】某高校在今年的自主招生考试成绩中随机抽取 100 名考生的笔试成绩,分为 5 组制出频率分布直方图如图所示.
组号 | 分组 | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 35 | 0.35 |
3 |
|
|
|
4 |
|
|
|
5 |
| 10 | 0.1 |
(1)求![]() 的值.
的值.
(2)该校决定在成绩较好的 、4、5 组用分层抽样抽取 6 名学生进行面试,则每组应各抽多少名学生?
(3)在(2)的前提下,从抽到 6 名学生中再随机抽取 2 名被甲考官面试,求这 2 名学生来自同一组的概率.
【答案】(1)见解析(2)3,2,1(3)![]()
【解析】试题分析:(1)利用频率分布表能求![]() 的值.
的值.
(2)三个组共有60人,从而利用分层抽样抽样方法抽取6名学生第三组应抽3人,第四组应抽2 人,第五组应抽1 人.
(3)记第三组抽出的3人分别a,b,c,第四组抽出的2人分别![]() 第五组抽出的1人为f,从这6人中随机抽取2人,利用列举法能求出2人来自同一组的概率.
第五组抽出的1人为f,从这6人中随机抽取2人,利用列举法能求出2人来自同一组的概率.
试题解析:
(1)由题意得![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
(2)三个组共有 60 人,所以第三组应抽![]() 人,第四组应抽
人,第四组应抽![]() 人,第五组应抽
人,第五组应抽![]() 人.
人.
(3)记第三组抽出的 3 人分别为![]() ,第四组抽出的 2 人分别为
,第四组抽出的 2 人分别为![]() ,第五组抽出的1 人为
,第五组抽出的1 人为![]() ,从这 6 人中随机抽取 2 人,基本事件包含
,从这 6 人中随机抽取 2 人,基本事件包含
![]()
![]() ,共 15 个基本事件.
,共 15 个基本事件.
其中 2 人来自同一组的情况有![]() ,共 4 种.
,共 4 种.
所以,2 人来自同一组的概率为![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位编著. 《算法统宗》对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,以“竹筒容米”就是其中一首:家有九节竹一茎,为因盛米不均平;下头三节三升九,上梢四节贮三升;唯有中间二节竹,要将米数次第盛;若是先生能算法,也教算得到天明!大意是:用一根9节长的竹子盛米,每节竹筒盛米的容积是不均匀的.下端3节可盛米3.9升,上端4节可盛米3升,要按每节依次盛容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出中间两节的容积为( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的是( )
A. 由独立性检验可知,有 99%的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有 99%的可能物理优秀;
B. 两个随机变量相关系越强,则相关系数的绝对值越接近于 0;
C. 在线性回归方程![]() 中,当变量
中,当变量![]() 每增加一十单位时,变量
每增加一十单位时,变量![]() 平均增加 0.2 个单位;
平均增加 0.2 个单位;
D. 线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点.
至少经过其样本数据点中的一个点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下表:
加工零件个数x/个 | 10 | 20 | 30 | 40 | 50 |
加工时间y/分钟 | 64 | 69 | 75 | 82 | 90 |
经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数x与加工时间y这两个变量,下列判断正确的是( )
A. 成正相关,其回归直线经过点(30,75)
B. 成正相关,其回归直线经过点(30,76)
C. 成负相关,其回归直线经过点(30,76)
D. 成负相关,其回归直线经过点(30,75)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 为正三角形,且平面
为正三角形,且平面![]()
![]() 平面,
平面, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角大小
的平面角大小![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线从点A(-3,4)射出,到x轴上的点B后,被x轴反射到y轴上的点C,又被y轴反射,这时反射光线恰好过点D(-1,6),求光线BC所在直线的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于( )
A.6
B.7
C.8
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com