
已知函数 .
.
(1)解关于 的不等式
的不等式 ;
;
(2)若 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(1)当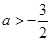 时,原不等式的解集为
时,原不等式的解集为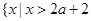 或
或 ;当
;当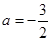 时,解集为
时,解集为 且
且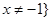 ;当
;当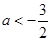 时,解集为
时,解集为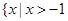 或
或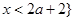 ;(2)
;(2) 的取值范围是
的取值范围是 .
.
解析试题分析:(1)本小题是含参数 的一元二次不等式问题,求解时先考虑因式分解,后针对根的大小进行分类讨论,分别写出不等式的解集即可;(2)不等式的恒成立问题,一般转化为函数的最值问题,不等式
的一元二次不等式问题,求解时先考虑因式分解,后针对根的大小进行分类讨论,分别写出不等式的解集即可;(2)不等式的恒成立问题,一般转化为函数的最值问题,不等式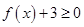 即
即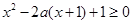 在
在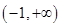 上恒成立可转化为
上恒成立可转化为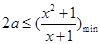 (
(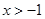 ),而函数
),而函数 的最小值可通过均值不等式进行求解,从而可求得
的最小值可通过均值不等式进行求解,从而可求得 的取值范围.
的取值范围.
试题解析:(1)由 得
得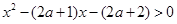 ,即
,即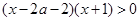 1分
1分
当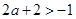 ,即
,即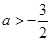 时,原不等式的解为
时,原不等式的解为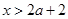 或
或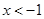 3分
3分
当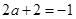 ,即
,即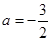 时,原不等式的解为
时,原不等式的解为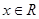 且
且 4分
4分
当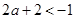 ,即
,即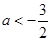 时,原不等式的解为
时,原不等式的解为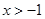 或
或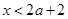
综上,当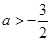 时,原不等式的解集为
时,原不等式的解集为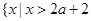 或
或 ;当
;当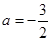 时,解集为
时,解集为 且
且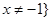 ;当
;当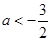 时,解集为
时,解集为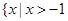 或
或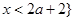 6分
6分
(2)由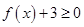 得
得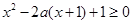 在
在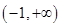 上恒成立,即
上恒成立,即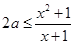 在
在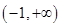 上恒成立,所以
上恒成立,所以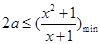 (
(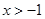 ) 8 分
) 8 分
令 ,则
,则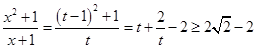 10分
10分
当且仅当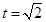 等号成立
等号成立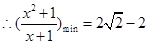

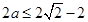 ,即
,即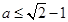
故实数 的取值范围是
的取值范围是 12分.
12分.
考点:1.一元二次含参不等式;2.分类讨论的思想;3.分离参数法;4.均值不等式.


科目:高中数学 来源: 题型:解答题
已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设函数f(x)= .
.
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]时有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (其中
(其中 且
且 ),
), 是
是 的反函数.
的反函数.
(1)已知关于 的方程
的方程 在区间
在区间 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围;
(2)当 时,讨论函数
时,讨论函数 的奇偶性和增减性;
的奇偶性和增减性;
(3)设 ,其中
,其中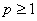 .记
.记 ,数列
,数列 的前
的前 项的和为
项的和为 (
( ),
),
求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( ).
).
(1)证明:当 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数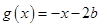 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 的定义域是
的定义域是 ,对于任意的
,对于任意的 ,有
,有 ,且当
,且当 时,
时, .
.
(1)求 的值;
的值;
(2)判断函数的奇偶性;
(3)用函数单调性的定义证明函数 为增函数;
为增函数;
(4)若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录.为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足 (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=
(1)若f(-1)=0,且函数f(x) ≥0的对任意x属于一切实数成立,求F(x)的表达式;
(2)在 (1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com