练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，四棱锥V﹣ABCD中，底面ABCD是菱形，对角线AC与BD交于点O，VO⊥平面ABCD，E是棱VC的中点．

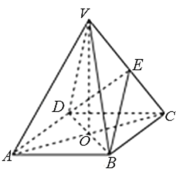
    （1）求证：VA∥平面BDE；

    （2）求证：平面VAC⊥平面BDE．

    【答案】（1）见解析（2）见解析

    【解析】

    （1）连结OE，证明VA∥OE得到答案.

    （2）证明VO⊥BD，BD⊥AC，得到BD⊥平面VAC，得到证明.

    （1）连结OE．因为底面ABCD是菱形，所以O为AC的中点，

    又因为E是棱VC的中点，所以VA∥OE，又因为OE平面BDE，VA平面BDE，

    所以VA∥平面BDE；

    （2）因为VO⊥平面ABCD，又BD平面ABCD，所以VO⊥BD，

    因为底面ABCD是菱形，所以BD⊥AC，又VO∩AC＝O，VO，AC平面VAC，

    所以BD⊥平面VAC．又因为BD平面BDE，所以平面VAC⊥平面BDE．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）已知直线：，：若直线与关于对称，又函数在处的切线与平行，求实数的值；

    （2）若，证明：当时，恒成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的右顶点为，左焦点为，离心率为，已知也是抛物线的焦点， 到准线的距离为

    （1）求椭圆的方程和抛物线的方程；

    （2）过原点的直线交于两点，点在第一象限，轴，垂足为，交于另一点.

    ①证明：三点共线

    ②求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知符号函数sgnx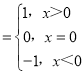f（x）是定义在R上的减函数，g（x）＝f（x）﹣f（ax）（a＞1），则（ ）

    A.sgn[g（x）]＝sgn xB.sgn[g（x）]＝﹣sgnx

    C.sgn[g（x）]＝sgn[f（x）]D.sgn[g（x）]＝﹣sgn[f（x）]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线E：y2＝2px（p＞0），焦点F到准线的距离为3，抛物线E上的两个动点A（x1，y1）和B（x2，y2），其中x1≠x2且x1+x2＝4．线段AB的垂直平分线与x轴交于点 C．

    （1）求抛物线E的方程；

    （2）求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2＋ax＋b，g(x)＝ex(cx＋d)，若曲线y＝f(x)和曲线y＝g(x)都过点P(0，2)，且在点P处有相同的切线y＝4x＋2．

    (1)求a，b，c，d的值；

    (2)若x≥－2时，恒有f(x)≤kg(x)，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）讨论的单调性；

    （Ⅱ）若有两个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点在椭圆上.

    （1）求椭圆的方程；

    （2）过椭圆的右焦点作互相垂直的两条直线、，其中直线交椭圆于两点，直线交直线于点，求证：直线平分线段.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若在定义域上不单调，求的取值范围；

    （2）设分别是的极大值和极小值，且，求的取值范围.

    查看答案和解析>>

    同步练习册答案