
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)先求得![]() 再根据1,0,2a的大小进行分类确定
再根据1,0,2a的大小进行分类确定![]() 的单调性;(Ⅱ)借助第(Ⅰ)问的结论,通过分类讨论函数的单调性,确定零点个数,从而可得a的取值范围为
的单调性;(Ⅱ)借助第(Ⅰ)问的结论,通过分类讨论函数的单调性,确定零点个数,从而可得a的取值范围为![]() .
.
试题解析:(Ⅰ)![]()
(Ⅰ)设![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以f(x)在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(Ⅱ)设![]() ,由
,由![]() 得x=1或x=ln(-2a).
得x=1或x=ln(-2a).
①若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增.
单调递增.
②若![]() ,则ln(-2a)<1,故当
,则ln(-2a)<1,故当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
③若![]() ,则
,则![]() ,故当
,故当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(Ⅱ)(Ⅰ)设![]() ,则由(Ⅰ)知,
,则由(Ⅰ)知,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又![]() ,取b满足b<0且
,取b满足b<0且![]() ,
,
则![]() ,所以
,所以![]() 有两个零点.
有两个零点.
(Ⅱ)设a=0,则![]() ,所以
,所以![]() 只有一个零点.
只有一个零点.
(iii)设a<0,若![]() ,则由(Ⅰ)知,
,则由(Ⅰ)知,![]() 在
在![]() 单调递增.
单调递增.
又当![]() 时,
时,![]() <0,故
<0,故![]() 不存在两个零点;若
不存在两个零点;若![]() ,则由(Ⅰ)知,
,则由(Ⅰ)知,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.又当
单调递增.又当![]() 时
时![]() <0,故
<0,故![]() 不存在两个零点.
不存在两个零点.
综上,a的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】举行动物运动会其中有小兔大兔接力赛跑一项,跑道从起点![]() 经过点
经过点![]() 再到终点
再到终点![]() ,其中
,其中![]() 米,
米,![]() 米,规定小兔跑第一棒从
米,规定小兔跑第一棒从![]() 到
到![]() ,大兔在
,大兔在![]() 处接力完成跑第二棒从
处接力完成跑第二棒从![]() 到
到![]() ,假定接力赛跑时小兔大兔的各自速度都是均匀的,且它们的速度之和为定值10米/秒,试问小兔和大兔应以怎样的速度接力赛跑,才能使接力赛成绩最好(所需时间最短),并求其最短时间.
,假定接力赛跑时小兔大兔的各自速度都是均匀的,且它们的速度之和为定值10米/秒,试问小兔和大兔应以怎样的速度接力赛跑,才能使接力赛成绩最好(所需时间最短),并求其最短时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.
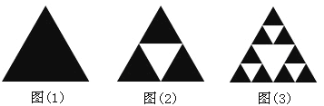
现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
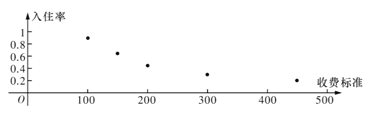
【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天,这五家“农家乐的收费标准互不相同得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
(1)若从以上五家“农家乐”中随机抽取两家深人调查,记![]() 为“入住率超过0.6的农家乐的个数,求
为“入住率超过0.6的农家乐的个数,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,
哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,![]() 的结果精确到0.1)
的结果精确到0.1)
(3)根据第(2)问所求的回归方程,试估计收费标准为多少时,100天销售额L最大?(100天销售额L=100×入住率×收费标准x)
参考数据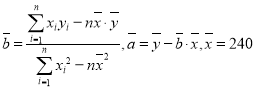 ,
,![]() ,
,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右两焦点分别为
的左右两焦点分别为![]() 、
、![]() .
.
(1)若矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 均在
均在![]() 上,求该矩形绕
上,求该矩形绕![]() 轴旋转一周所得圆柱侧面积
轴旋转一周所得圆柱侧面积![]() 的取值范围;
的取值范围;
(2)设斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() (
(![]() ),求证:
),求证:![]() ;
;
(3)过![]() 上一动点
上一动点![]() 作直线
作直线![]() ,其中
,其中![]() ,过
,过![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:集合
满足:集合![]() 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数![]() 是等比源函数.
是等比源函数.
(![]() )判断下列函数:①
)判断下列函数:①![]() ;②
;②![]() ;③
;③![]() 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(![]() )判断函数
)判断函数![]() 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
(![]() )证明:
)证明: ![]() ,
, ![]() ,函数
,函数![]() 都是等比源函数.
都是等比源函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com