练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】举行动物运动会其中有小兔大兔接力赛跑一项，跑道从起点经过点再到终点，其中米，米，规定小兔跑第一棒从到，大兔在处接力完成跑第二棒从到，假定接力赛跑时小兔大兔的各自速度都是均匀的，且它们的速度之和为定值10米/秒，试问小兔和大兔应以怎样的速度接力赛跑，才能使接力赛成绩最好（所需时间最短），并求其最短时间.

    【答案】小兔和大兔应分别以米/秒、米/秒的速度接力赛跑，到达终点最快时间为9秒.

    【解析】

    设出小兔大兔的速度，构造基本不等式求解即可.

    设小兔和大兔应分别以x米/秒、y米/秒的速度接力赛跑，则由题意知x+y=10，

    问题相当于求解的最小值，

    =（x+y）=，当且仅当，即y=2x=时等号成立，

    所以小兔和大兔应分别以米/秒、米/秒的速度接力赛跑，到达终点最快时间为9秒.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若有穷数列（）满足：①；②.则称该数列为“阶非凡数列”

    （1）分别写出一个单调递增的“阶非凡数列”和一个单调递减的“阶非凡数列”；

    （2）设，若“阶非凡数列”是等差数列，求其通项公式；

    （3）记“阶非凡数列”的前项的和为，求证：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于曲线所在的平面上的定点，若存在以点为顶点的角，使得对于曲线上的任意两个不同的点恒成立，则称角为曲线的“点视角”，并称其中最小的“点视角”为曲线相对于点的”点确视角”.已知曲线和圆是轴上一点

    （1）对于坐标原点，写出曲线的“点确视角”的大小；

    （2）若在曲线上，求的最小值；

    （3）若曲线和圆的“点确视角”相等，求点坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求函数的单调区间；

    （2）讨论函数的零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）当b=0时，求函数的极小值；

    （2）若已知b>1且函数与直线y=-x相切，求b的值；

    （3）在（2）的条件下，函数与直线y=-x+m有三个公共点，求m的取值范围.(直接写出答案)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，侧棱底面，底面是直角梯形，∥，，且，，是棱的中点 ．

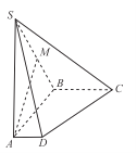
    （Ⅰ）求证：∥平面；

    （Ⅱ）求平面与平面所成锐二面角的余弦值；

    （Ⅲ）设点是线段上的动点，与平面所成的角为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）当时，求函数的单调区间；

    （2）设函数，若，且在上恒成立，求的取值范围；

    （3）设函数，若，且在上存在零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具，它由五块等腰直角三角形，一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道：近又有七巧图，其式五，其数七，其变化之式多至千余.体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之.如图是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自阴影部分的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）讨论的单调性；

    （Ⅱ）若有两个零点，求的取值范围.

    查看答案和解析>>

    同步练习册答案