
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点 .
的中点 .
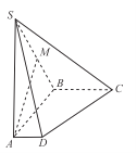
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②运动会的工作人员为参加![]() 接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样B.系统抽样、简单随机抽样、分层抽样
C.简单随机抽样、简单随机抽样、分层抽样D.系统抽样、分层抽样、简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“节能减排,绿色生态”为当今世界各国所倡导,某公司在科研部门的鼎力支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该公 司每月的处理量![]() (吨)至少为50吨,至多为220吨.月处理成本
(吨)至少为50吨,至多为220吨.月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系式近似表示为:
(吨)之间的函数关系式近似表示为:![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为120元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为120元.
(1)该公司每月处理量为多少吨时,才能使每吨的平均处理成本![]() 最低?
最低?
(2)每月处理量为多少吨时,月获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
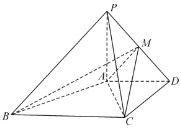
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为45°,如果存在,求
的大小为45°,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com