
【题目】函数![]()
(1)讨论函数![]() 的单凋性;
的单凋性;
(2)若存在![]() 使得对任意的
使得对任意的![]() 不等式
不等式![]() (其中e为自然对数的底数)都成立,求实数
(其中e为自然对数的底数)都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)略;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)求导,讨论参数的取值确定导函数的正负,进而判定函数的单调性;(Ⅱ)先借助(Ⅰ)的结论求出不等式左边的最小值,即将存在性问题转化为左边的最小值大于不等式右边,再作差构造函数,将不等式恒成立问题转化为求函数的最值问题.
试题解析:(I)![]()
![]() ,记
,记![]()
(i)当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(ii)当![]() 时,因为
时,因为![]() ,
,
所以![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(iii)当![]() 时,由
时,由![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增
上单调递增
(II)由(I)知当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 的最大值是
的最大值是![]() ,对任意的
,对任意的![]() ,
,
都存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
等价于对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
即对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
记![]() ,由
,由![]() ,
,
![]() ,
,
由![]() 得
得![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
①当![]() 时,
时,![]() ,且
,且![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 时,
时,![]() 恒成立;
恒成立;
②当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
此时![]() 单调递增,且
单调递增,且![]() ,
,
所以![]() 时,
时,![]() 成立;
成立;
③当![]() 时,
时,![]() ,
,![]() ,
,
所以存在![]() 使得
使得![]() ,因此
,因此![]() 不恒成立.
不恒成立.
综上,![]() 的取值范围是
的取值范围是![]() .
.
另解(II)由(Ⅰ)知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 时,函数
时,函数![]() 的最大值是
的最大值是![]() ,
,
对任意的![]() ,都存在
,都存在![]() ,
,
使得不等式![]() 成立,
成立,
等价于对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
即对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
记![]() ,
,
由![]() ,且
,且![]()
∴对任意的![]() ,不等式
,不等式![]() 都成立的必要条件为
都成立的必要条件为![]()
又![]() ,
,
由![]() 得
得![]() 或
或![]()
因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 时,
时,![]() 恒成立;
恒成立;
②当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
此时![]() 单调递增,且
单调递增,且![]() ,
,
所以![]() 时,
时,![]() 成立.
成立.
综上,![]() 的取值范围是
的取值范围是![]()


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,平行四边形![]() 所在平面与直角梯形
所在平面与直角梯形![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
,![]() 为
为![]() 中点.
中点.
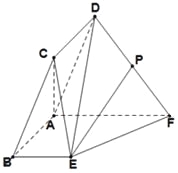
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点 .
的中点 .
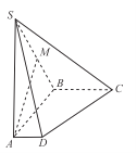
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.

(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,圆
,圆![]() 是以
是以![]() 的中点为圆心,
的中点为圆心,![]() 为半径的圆.
为半径的圆.
(1)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;
(2)若![]() 是圆
是圆![]() 外一点,从
外一点,从![]() 向圆
向圆![]() 引切线
引切线![]() ,
,![]() 为切点,
为切点,![]() 为坐标原点,
为坐标原点,![]() ,求使
,求使![]() 最小的点
最小的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区观众对某类休育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
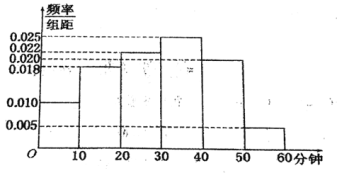
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(1)根据已知条件完成下面的![]() 列联表,并据此资料判断是否有
列联表,并据此资料判断是否有![]() 的把握认为“体育迷”与性别有关?
的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将日均收看读体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
附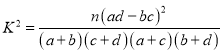 .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com