
【题目】设函数![]() .
.
(1)当b=0时,求函数![]() 的极小值;
的极小值;
(2)若已知b>1且函数![]() 与直线y=-x相切,求b的值;
与直线y=-x相切,求b的值;
(3)在(2)的条件下,函数![]() 与直线y=-x+m有三个公共点,求m的取值范围.(直接写出答案)
与直线y=-x+m有三个公共点,求m的取值范围.(直接写出答案)
科目:高中数学 来源: 题型:
【题目】上海途安型号出租车价格规定:起步费![]() 元,可行
元,可行![]() 千米;
千米;![]() 千米以后按每千米按
千米以后按每千米按![]() 元计价,可再行
元计价,可再行![]() 千米;以后每千米都按
千米;以后每千米都按![]() 元计价。假如忽略因交通拥挤而等待的时间.
元计价。假如忽略因交通拥挤而等待的时间.
![]() 请建立车费
请建立车费![]() (元)和行车里程
(元)和行车里程![]() (千米)之间的函数关系式;
(千米)之间的函数关系式;
![]() 注意到上海出租车的计价系统是以元为单位计价的,如:小明乘坐途安型号出租车从华师大二附中本部到浦东实验学校走路线一(路线一总长
注意到上海出租车的计价系统是以元为单位计价的,如:小明乘坐途安型号出租车从华师大二附中本部到浦东实验学校走路线一(路线一总长![]() 千米)须付车费
千米)须付车费![]() 元,走路线二(路线二总长
元,走路线二(路线二总长![]() 千米)也须付车费
千米)也须付车费![]() 元.将上述函数解析式进行修正(符号
元.将上述函数解析式进行修正(符号![]() 表示不大于
表示不大于![]() 的最大整数,符号
的最大整数,符号![]() 表示不小于
表示不小于![]() 的最小整数);并求小明乘坐途安型号出租车从华师大二附中本部到闵行分校须付车费多少元?(注:两校区路线长
的最小整数);并求小明乘坐途安型号出租车从华师大二附中本部到闵行分校须付车费多少元?(注:两校区路线长![]() 千米)
千米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 、
、![]() .
.
(1)求以![]() 为焦点,原点为顶点的抛物线方程;
为焦点,原点为顶点的抛物线方程;
(2)若椭圆![]() 上点
上点![]() 满足
满足![]() ,求
,求![]() 的纵坐标
的纵坐标![]() ;
;
(3)设![]() ,若椭圆
,若椭圆![]() 上存在两个不同点
上存在两个不同点![]() 、
、![]() 满足
满足![]() ,证明:直线
,证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象的顶点坐标为
的图象的顶点坐标为![]() ,且过坐标原点
,且过坐标原点![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在数列![]() 中是否存在这样一些项:
中是否存在这样一些项:![]()
![]()
![]() ,这些项都能够构成以
,这些项都能够构成以![]() 为首项,
为首项,![]() 为公比的等比数列
为公比的等比数列![]() ?若存在,写出
?若存在,写出![]() 关于
关于![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为提高生产质量,引入了一批新的生产设备,为了解生产情况,随机抽取了新、旧设备生产的共200件产品进行质量检测,统计得到产品的质量指标值如下表及图(所有产品质量指标值均位于区间![]() 内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
质量指标 | 频数 |
| 2 |
| 8 |
| 10 |
| 30 |
| 20 |
| 10 |
合计 | 80 |
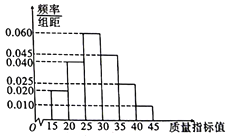
(1)根据上述图表完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为产品质量高与引人新设备有关;
的把握认为产品质量高与引人新设备有关;
新旧设备产品质量![]() 列联表
列联表
产品质量高 | 产品质量一般 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
(2)从旧设备生产的质量指标值位于区间![]() 的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于
的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于![]() 的概率.
的概率.
附: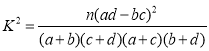 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】举行动物运动会其中有小兔大兔接力赛跑一项,跑道从起点![]() 经过点
经过点![]() 再到终点
再到终点![]() ,其中
,其中![]() 米,
米,![]() 米,规定小兔跑第一棒从
米,规定小兔跑第一棒从![]() 到
到![]() ,大兔在
,大兔在![]() 处接力完成跑第二棒从
处接力完成跑第二棒从![]() 到
到![]() ,假定接力赛跑时小兔大兔的各自速度都是均匀的,且它们的速度之和为定值10米/秒,试问小兔和大兔应以怎样的速度接力赛跑,才能使接力赛成绩最好(所需时间最短),并求其最短时间.
,假定接力赛跑时小兔大兔的各自速度都是均匀的,且它们的速度之和为定值10米/秒,试问小兔和大兔应以怎样的速度接力赛跑,才能使接力赛成绩最好(所需时间最短),并求其最短时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天,这五家“农家乐的收费标准互不相同得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
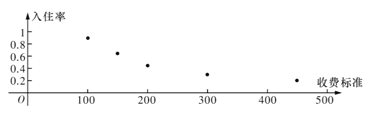
(1)若从以上五家“农家乐”中随机抽取两家深人调查,记![]() 为“入住率超过0.6的农家乐的个数,求
为“入住率超过0.6的农家乐的个数,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,
哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,![]() 的结果精确到0.1)
的结果精确到0.1)
(3)根据第(2)问所求的回归方程,试估计收费标准为多少时,100天销售额L最大?(100天销售额L=100×入住率×收费标准x)
参考数据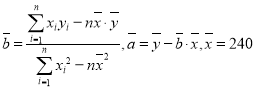 ,
,![]() ,
,![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com