
【题目】已知函数![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
(1)求证: ![]()
(2)若不等式![]() 在
在![]() 上恒成立,求正数
上恒成立,求正数![]() 的取值范围.
的取值范围.
【答案】(1)见证明; (2) ![]()
【解析】
(1)要证ex≥x+1,只需证f(x)=ex﹣x﹣1≥0,求导得f′(x)=ex﹣1,利用导数性质能证明ex≥x+1.
(2)不等式f(x)>ax﹣1在x∈[![]() ,2]上恒成立,即a
,2]上恒成立,即a![]() 在x∈[
在x∈[![]() ]上恒成立,令g(x)
]上恒成立,令g(x)![]() ,x∈[
,x∈[![]() ],利用导数性质求g(x)
],利用导数性质求g(x)![]() 在x∈[
在x∈[![]() ]上的最小值,由此能求出正数a的取值范围.
]上的最小值,由此能求出正数a的取值范围.
(1)由题意知,要证![]() ,只需证
,只需证![]() ,
,
求导得![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴f(x)在![]() 是增函数,在
是增函数,在![]() 时是减函数,
时是减函数,
即![]() 在
在![]() 时取最小值
时取最小值![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
(2)不等式![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
亦即![]() 在x∈[
在x∈[![]() ,2]上恒成立,令g(x)=
,2]上恒成立,令g(x)=![]() ,
,![]() ,
,
以下求![]() 在
在![]() 上的最小值,
上的最小值,
![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() ]时,
]时,![]() ,
,
∴当![]() ]时,
]时,![]() 单调递减,当
单调递减,当![]() ]时,
]时,![]() 单调递增,
单调递增,
∴![]() 在
在![]() 处取得最小值为
处取得最小值为![]() ,
,
∴正数a的取值范围是![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
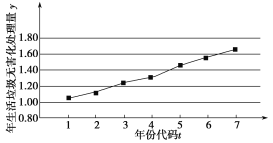
【题目】如图是我国2012年至2018年生活垃圾无害化处理量(单位:亿吨)的折线图.注:年份代码1~7分别对应年份2012~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数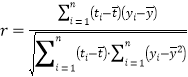 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为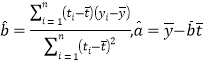 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用
的关系,可选用
A.一次函数B.二次函数
C.指数型函数D.对数型函数
查看答案和解析>>
科目:高中数学 来源: 题型:
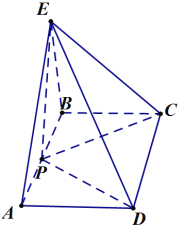
【题目】如图,在矩形ABCD中,AB=2BC,P是线段AB中点,![]() 平面ABCD.
平面ABCD.
(1)求证:![]() 平面EPC;
平面EPC;
(2)问在EP上是否存在点F,使平面![]() 平面BFC?若存在,求出
平面BFC?若存在,求出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出x(万元)与销售额y(万元)之间有如下的对应数据:

(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入y的值.
注:①参考公式:线性回归方程系数公式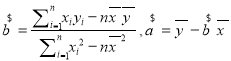 ;
;
②参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com