Question

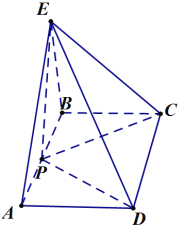
【题目】如图,在矩形ABCD中,AB=2BC,P是线段AB中点,平面ABCD.

(1)求证:平面EPC;

(2)问在EP上是否存在点F,使平面平面BFC?若存在,求出的值;若不存在请说明理由.

Answer 1

【答案】（1）详见解析；（2）存在，，理由见解析.

【解析】

（1）由已知得∠APD＝∠BPC＝45°，∠DPC＝90°，从而DP⊥PC，由EP⊥平面ABCD，得EP⊥DP，由此能证明DP⊥平面EPC．

（2）假设存在F，使平面AFD⊥平面BFC，由已知得AD∥平面BFC，从而AD平行于平面AFD与平面BFC的交线l，由已知得EP⊥AD，而AD⊥AB，从而l⊥平面FAB，∠AFB为平面AFD与平面BFC所成二面角的平面角，由此能求出当时，平面AFD⊥平面BFC．

解：（1）证明：∵在矩形ABCD中，AB＝2BC，

P、Q分别是线段AB，CD中点，

∴∠APD＝∠BPC＝45°，∴∠DPC＝90°，∴DP⊥PC，

∵EP⊥平面ABCD，DP平面ABCD，

∴EP⊥DP，

又PC∩EP＝P，∴DP⊥平面EPC．

（2）解：假设存在F，使平面AFD⊥平面BFC，

∵AD∥BC，BC平面BFC，AD不包含于平面BFC，

∴AD∥平面BFC，

∴AD平行于平面AFD与平面BFC的交线l，

∵EP⊥平面ABCD，

∴EP⊥AD，而AD⊥AB，

AB∩EP＝P，∴AD⊥平面EAB，∴l⊥平面FAB，

∴∠AFB为平面AFD与平面BFC所成二面角的平面角，

∵P是AB的中点，且FP⊥AB，

∴当∠AFB＝90°时，FP＝AP，

∴当时，平面AFD⊥平面BFC．