
【题目】若函数![]() 满足:集合
满足:集合![]() 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数![]() 是等比源函数.
是等比源函数.
(![]() )判断下列函数:①
)判断下列函数:①![]() ;②
;②![]() ;③
;③![]() 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(![]() )判断函数
)判断函数![]() 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
(![]() )证明:
)证明: ![]() ,
, ![]() ,函数
,函数![]() 都是等比源函数.
都是等比源函数.
【答案】(![]() )①②③均为等比源函数.(
)①②③均为等比源函数.(![]() )函数
)函数![]() 不是等比源函数(
不是等比源函数(![]() )见解析
)见解析
【解析】试题分析:(1)直接举例说明题目给出的三个函数都是“等比源函数”;(2)利用反证法思想,假设存在正整数![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,是
,是![]() ,
, ![]() ,
, ![]() 成等比数列,推出矛盾,从而证明函数f(x)=2x+1不是等比源函数;(3)首先证明数列{g(n)}为等差数列,然后验证g(1),g[g(1)+1],g[2g(1)+g(1)d+1]构成等比数列,从而说明结论的正确性.
成等比数列,推出矛盾,从而证明函数f(x)=2x+1不是等比源函数;(3)首先证明数列{g(n)}为等差数列,然后验证g(1),g[g(1)+1],g[2g(1)+g(1)d+1]构成等比数列,从而说明结论的正确性.
试题解析:
(![]() )①当
)①当![]() 取
取![]() ,
, ![]() ,
, ![]() 时,
时, ![]() 得
得![]() ,
, ![]() ,
, ![]() 构成等比数列,∴
构成等比数列,∴![]() 是等比源函数.
是等比源函数.
②当![]() 取
取![]() ,
, ![]() ,
, ![]() 时,
时, ![]() 得
得![]() ,
, ![]() ,
, ![]() 构成等比数列,∴
构成等比数列,∴![]() 是等比源函数.
是等比源函数.
③当![]() 取
取![]() ,
, ![]() ,
, ![]() 时,
时, ![]() 得
得![]() ,
, ![]() ,
, ![]() 构成等比数列,∴
构成等比数列,∴![]() 是等比源函数.
是等比源函数.
综上①②③均为等比源函数.
(![]() )函数
)函数![]() 不是等比源函数,
不是等比源函数,
证明如下:
假设存在正整数![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,是
,是![]() ,
, ![]() ,
, ![]() 成等比数列,∴
成等比数列,∴![]() ,
,
![]() ,∴
,∴![]() ,等式两边同除以
,等式两边同除以![]() ,
,
∴![]() ,又∵
,又∵![]() ,
, ![]() ,
,
∴等式左边为偶数,等式右边为奇数,∴![]() 不可能成立,
不可能成立,
故假设不成立,
∴![]() 不是等比源函数.
不是等比源函数.
(![]() )证明:∵
)证明:∵![]() ,
, ![]() ,都有
,都有![]() ,
,
∴![]() ,
, ![]() ,数列
,数列![]() 都是以
都是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,
的等差数列,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等比数列,
成等比数列,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,函数
,函数![]() 都是等比源函数.
都是等比源函数.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示. (Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?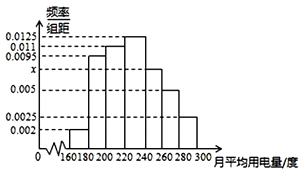
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣3|+|x﹣4|. (Ⅰ)解不等式f(x)≤2;
(Ⅱ)若对任意实数x∈[5,9],f(x)≤ax﹣1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]()
(1)若![]() ,求
,求![]() 的值;
的值;
(2)令![]() ,把函数
,把函数![]() 的图象上每一点的横坐标都缩小为原来的一半(纵坐标不变),再把所得图象沿
的图象上每一点的横坐标都缩小为原来的一半(纵坐标不变),再把所得图象沿![]() 轴向左平移
轴向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调增区间即图象的对称中心.
的单调增区间即图象的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A= ![]() ,B={y|y=log2x,4<x<16},
,B={y|y=log2x,4<x<16}, 
(1)求图中阴影部分表示的集合C;
(2)若非空集合D={x|4﹣a<x<a},且D(A∪B),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3sin(ωx+) ![]() 的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( ) 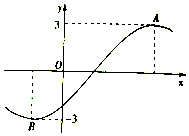
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com