
���� ��1�����ü�������ֱ������Ļ����������ɵ�ֱ��C1��ֱ�����귽�̺�ԲC2��Բ�ĵļ����ꣻ
��2�����Բ�ĵ�ֱ�ߵľ��룬���ù��ɶ��������߶�AB�ij���
��� �⣺��1����ֱ��C1�ļ����귽��Ϊ��cos��-��sin��+1=0��
��ֱ��C1��ֱ�����귽��Ϊx-y+1=0��
������C2�IJ�������Ϊ$\left\{\begin{array}{l}{x=-1+2cos��}\\{y=\sqrt{3}+2sin��}\end{array}\right.$����Ϊ��������
����ͨ����Ϊ��x+1��2+��y-$\sqrt{3}$��2=4��
��ԲC2��Բ�ĵ�ֱ������Ϊ��-1��$\sqrt{3}$���������꣨2��$\frac{2��}{3}$����
��2����ֱ��C1��ԲC2�Ľ���ΪA��B����-1��$\sqrt{3}$����ֱ��x-y+1=0�ľ���d=$\frac{|-1-\sqrt{3}+1|}{\sqrt{2}}$=$\frac{\sqrt{3}}{\sqrt{2}}$��
���߶�AB�ij�2$\sqrt{4-\frac{3}{2}}$=$\sqrt{10}$��
���� ���⿼����Բ�ļ����귽�̡��������̡��㵽ֱ�ߵľ��빫ʽ��������������������������������е��⣮


 С�����ϵ�д�
С�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��$\frac{3}{2}$�� | B�� | ��$\frac{1}{2}$��$\frac{3}{2}$] | C�� | ��$\frac{1}{2}$��$\frac{3}{2}$�� | D�� | ��$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
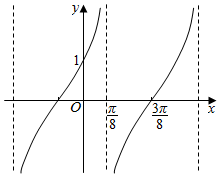 ��֪����f��x��=Atan����x+�գ�$���أ�0��|��|��\frac{��}{2}��$��y=f��x���IJ���ͼ����ͼ����$f��\frac{��}{24}��$=����������
��֪����f��x��=Atan����x+�գ�$���أ�0��|��|��\frac{��}{2}��$��y=f��x���IJ���ͼ����ͼ����$f��\frac{��}{24}��$=����������| A�� | 2+$\sqrt{3}$ | B�� | $\sqrt{3}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | 2-$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | ��ǩ�� | C�� | ϵͳ���� | D�� | �ֲ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com