
分析 由已知列式得到b,c与a的关系,把函数解析式用含有a的代数式表示.
(1)直接利用与正弦函数有关的复合函数的单调性求得f(x)的单调递减区间;
(2)设sin(x+$\frac{π}{4}$)=t,则y=$\sqrt{2}$(1-a)t+a,由x得范围得到t的范围,然后对1-a>0、1-a=0、1-a<0分类讨论求解得答案;
(3)由题意知a=8,则由mf(x)+nf(x-φ)=1得8(m+n)-7$\sqrt{2}$msin(x+$\frac{π}{4}$)-7$\sqrt{2}$nsin(x+$\frac{π}{4}$-φ)=1.令x+$\frac{π}{4}$=X,得8(m+n)-7$\sqrt{2}$(m+ncosφ)sinX+7$\sqrt{2}$nsinφcosX=1.
要使上式对任意X恒成立,则有$\left\{\begin{array}{l}{8(m+n)=1}\\{m+ncosφ=0}\\{nsinφ=0}\end{array}\right.$,由此求得答案.
解答 解:由题意可得,$\left\{\begin{array}{l}{f(0)=a+b=1}\\{f(\frac{π}{2})=a+c=1}\end{array}\right.$,则b=c=1-a,
∴f(x)=(1-a)(sinx+cosx)+a=$\sqrt{2}$(1-a)sin(x+$\frac{π}{4}$)+a.
(1)∵1-a=b>0,由2kπ+$\frac{π}{2}$<x+$\frac{π}{4}$<2kπ+$\frac{3π}{2}$,得:2kπ+$\frac{π}{4}$<x<2kπ+$\frac{5π}{4}$,
∴f(x)的递减区间为[2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$],k∈Z;
(2)设sin(x+$\frac{π}{4}$)=t,则y=$\sqrt{2}$(1-a)t+a,
∵$x∈(0,\frac{π}{2})$,
∴x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),则t∈($\frac{\sqrt{2}}{2}$,1],
①当1-a>0时,f(x)∈(1,$\sqrt{2}$(1-a)t+a],此时|f(x)|≤2恒成立,
只需$\sqrt{2}$(1-a)t+a≤2,得a∈[-$\sqrt{2}$,1);
②当1-a=0时,f(x)=1,满足题意;
②当1-a<0时,f(x)∈[$\sqrt{2}$(1-a)t+a,1),此时|f(x)|≤2恒成立,
只需$\sqrt{2}$(1-a)t+a≥-2,得a∈(1,4+3$\sqrt{2}$].
综上所述,a的取值范围为[-$\sqrt{2}$,4+3$\sqrt{2}$].
(3)可得a=8,则f(x)=8-7$\sqrt{2}$sin(x+$\frac{π}{4}$).
由mf(x)+nf(x-φ)=1得8(m+n)-7$\sqrt{2}$msin(x+$\frac{π}{4}$)-7$\sqrt{2}$nsin(x+$\frac{π}{4}$-φ)=1.
令x+$\frac{π}{4}$=X,得8(m+n)-7$\sqrt{2}$(m+ncosφ)sinX+7$\sqrt{2}$nsinφcosX=1.
要使上式对任意X恒成立,则有$\left\{\begin{array}{l}{8(m+n)=1}\\{m+ncosφ=0}\\{nsinφ=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{sinφ=0}\\{cosφ=1}\\{m=n=\frac{1}{16}}\end{array}\right.$.
所以m=$\frac{1}{16}$,n=$\frac{1}{16}$,φ=2kπ+π,k∈Z.
点评 本题考查三角函数值的恒等变换应用,考查y=Asin(ωx+φ)型函数的图象和性质,训练了函数恒成立问题的求解方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{25}{3}$ | C. | -89 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
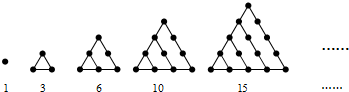
| A. | 35 | B. | 36 | C. | 45 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
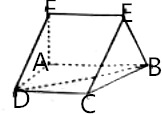 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD
如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e3f(-14)<f(-5),e3f(-10)<f(-19) | B. | e3f(-14)>f(-5),e3f(-10)>f(-19) | ||
| C. | e3f(-14)<f(-5),e3f(-10)>f(-19) | D. | e3f(-14)>f(-4),e3f(-10)<f(-19) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,2] | C. | [4,+∞) | D. | [2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com