练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体ABCD－A1B1C1D1中，M，N，P分别是C1C, C1B1，C1D1的中点，点H在四边形A1ADD1的边及其内部运动，则H满足条件________时，有BH∥平面MNP.

    【答案】线段

    【解析】

    推导出PN∥BD，PM∥A1B，MN∥A1D，从而平面A1BD∥平面PMN，从而求出H满足条件H∈线段A1D时，有BH∥平面MNP．

    H∈线段A1D.理由如下，

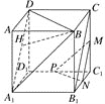
    连接A1B，A1D，BD，CB1,

    因为M，N分别是C1C, C1B1的中点，

    所以MN∥CB1，

    因为CD∥A1B1，且CD＝A1B1，

    所以四边形CDA1B1是平行四边形，所以CB1∥DA1，

    所以MN∥DA1，

    又MN平面A1BD，DA1平面A1BD，

    所以MN∥平面A1BD.

    同理可证PN∥平面A1BD，

    又MN平面MNP，PN平面MNP，MN∩PN＝N，

    所以平面A1BD∥平面MNP.

    又因为BH平面A1BD，所以BH∥平面MNP.

    故答案为：线段.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】执行如图的程序框图，则输出的s=（　　）

    A.
    B.-
    C.
    D.-

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的参数方程为（为参数）.以直角坐标系的原点为极点，轴的正半轴为极轴建立坐标系，曲线的极坐标方程为.

    （1）求的普通方程和的直角坐标方程；

    （2）若过点的直线与交于，两点，与交于，两点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义域为R的函数f（x）= ，则关于x的方程f2（x）+bf（x）+c=0有5个不同的实数解xi（i=1，2，3，4，5），则f（x1+x2+x3+x4+x5+2）=（ ）
    A.
    B.
    C.2
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设a∈R，函数f（x）=lnx﹣ax．
    （1）若a=2，求曲线y=f（x）在P（1，﹣2）处的切线方程；
    （2）若f（x）无零点，求实数a的取值范围；
    （3）若f（x）有两个相异零点x1 ， x2 ， 求证：x1x2＞e2 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|3x﹣1|+ax+3
    （1）若a=1，解不等式f（x）≤4；
    （2）若函数f（x）有最小值，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出以下命题：
    ①双曲线 ﹣x2=1的渐近线方程为y=± x；
    ②命题P：x∈R+ ， sinx+ ≥1是真命题；
    ③已知线性回归方程为 =3+2x，当变量x增加2个单位，其预报值平均增加4个单位；
    ④设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=0.2，则P（﹣1＜ξ＜0）=0.6；
    则正确命题的序号为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}中，a1=1，an﹣an+1=anan+1 ， n∈N* ．
    （1）求数列{an}的通项公式；
    （2）Sn为{an}的前n项和，bn=S2n﹣Sn ， 求bn的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点,,直线与直线相交于点,直线与直线的斜率分别记为与,且．

    （1）求点的轨迹的方程；

    （2）过定点作直线与曲线交于两点, 的面积是否存在最大值？若存在,求出面积的最大值；若不存在,请说明理由．

    查看答案和解析>>

    同步练习册答案