
【题目】如图,某市拟在长为8 km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数![]() ,
,![]() 的图象,且图象的最高点为
的图象,且图象的最高点为![]() ;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定
;赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定![]() .
.
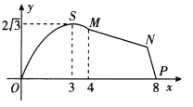
(1)求点M的坐标;
(2)应如何设计,才能使折线段赛道MNP最长?
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,斜率不为0的直线
,斜率不为0的直线![]() :
:![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若![]() 、
、![]() 分别是
分别是![]() 的左、右焦点,当
的左、右焦点,当![]() 经过
经过![]() 且
且![]() 时,求
时,求![]() 的值;
的值;
(2)试探究,是否存在点![]() ,使得
,使得![]() ?若存在,请写出满足条件的
?若存在,请写出满足条件的![]() 、
、![]() 的关系式;若不存在,说明理由.
的关系式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
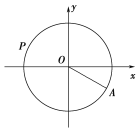
【题目】水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3![]() ,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<
,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<![]() ).则下列叙述错误的是( )
).则下列叙述错误的是( )
A.R=6,ω=![]() ,φ=-
,φ=-![]()
B.当t∈[35,55]时,点P到x轴的距离的最大值为6
C.当t∈[10,25]时,函数y=f(t)单调递减
D.当t=20时,|PA|=6![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,
在椭圆上,![]() 为原点.
为原点.
⑴若![]() ,
,![]() ,求椭圆的离心率;
,求椭圆的离心率;
⑵若椭圆的右顶点为![]() ,短轴长为2,且满足
,短轴长为2,且满足![]() 为椭圆的离心率).
为椭圆的离心率).
①求椭圆的方程;
②设直线![]() :
:![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,若
两点,若![]() 的面积为1,求实数
的面积为1,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com