考点:直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)通过取BC1的中点G,连接EG、A1G,先证得线线平行,再由线成平行的判定定理得到线面平行;
(2)建立空间坐标系,分别求出直线EF的方向向量与平面ABB1A1的法向量,代入向量夹角公式,可得答案.
解答:
证明:(1)取BC
1的中点G,连接EG、A
1G,
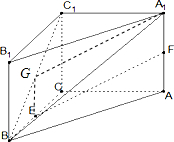
∵E、F分别是BC A
1A的中点.
∴EG∥CC
1,且EG=
CC
1,AF∥CC
1,且AF=
CC
1,
∴EG∥AF,且EG=AF,
∴四边形A
1GEF为平行四边形,
∴EF∥A
1G,
∵EF?平面A
1C
1B,A
1G?平面A
1C
1B,
∴EF∥平面A
1C
1B;
(2)∵直三棱柱ABC-A
1B
1C
1中,CA=CB=CC
1=2,∠ACB=90°,E、F分别是BC A
1A的中点.
故以C为坐标原点建立空间坐标系O-xyz,
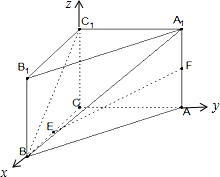
则A(0,2,0),B(2,0,0),E(1,0,0),F(0,2,1),C
1(0,0,2),
则
=(-1,2,1),
=(0,0,2),
=(2,-2,0),
设平面ABB
1A
1的法向量为
=(x,y,z),
则
,即
,
令x=1,则
=(1,1,0),
设直线EF与平面ABB
1A
1所成角为θ,
则sinθ=
=
=
故cosθ=
,
∴tanθ=
点评:本题考查的知识点是线面平行的判定定理,直线与平面的夹角,是空间线面关系的综合应用,难度中档.

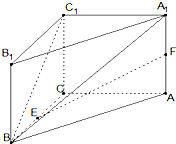 在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.
在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.



 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案